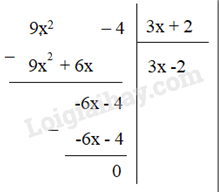Giải mục 2 trang 40, 41 SGK Toán 7 tập 2 - Kết nối tri thứcKiểm tra lại rằng ta có phép chia hết A : B = 2x^2 – 5x + 1, nghĩa là xảy ra A = B . (2x^2 – 5x + 1) Tổng hợp đề thi học kì 2 lớp 7 tất cả các môn - Kết nối tri thức Toán - Văn - Anh - Khoa học tự nhiên...
Lựa chọn câu để xem lời giải nhanh hơn
2. Chia đa thức cho đa thức, trường hợp chia hết Câu hỏi Kiểm tra lại rằng ta có phép chia hết A : B = 2x2 – 5x + 1, nghĩa là xảy ra A = B . (2x2 – 5x + 1) Phương pháp giải: Nhân đa thức B với đa thức 2x2 – 5x + 1. Nếu kết quả bằng đa thức A thì đúng Lời giải chi tiết: Ta có: B . (2x2 – 5x + 1) = (x2 – 4x – 3) . (2x2 – 5x + 1) = x2 .(2x2 – 5x + 1) – 4x . (2x2 – 5x + 1) – 3.(2x2 – 5x + 1) = x2 . 2x2 + x2 . (-5x) + x2 . 1 – [4x . 2x2 + 4x . (-5x) + 4x . 1] – [3.2x2 + 3.(-5x) + 3.1] = 2x4 – 5x3 + x2 – ( 8x3 – 20x2 + 4x) – (6x2 – 15x + 3) = 2x4 – 5x3 + x2 – 8x3 + 20x2 - 4x – 6x2 + 15x - 3 = 2x4 + (-5x3 – 8x3) + (x2 + 20x2 – 6x2 ) + (-4x + 15x) – 3 = 2x4 - 13x3 + 15x2 + 11x - 3 =A Vậy ta có phép chia hết A : B = 2x2 – 5x + 1 Luyện tập 2 Thực hiện phép chia: a) (-x6 + 5x4 – 2x3) : (0,5x2) b) (9x2 – 4) : (3x + 2) Phương pháp giải: Muốn chia đa thức A cho đa thức B, ta làm như sau: Bước 1: Đặt tính chia tương tự như chia hai số tự nhiên. Lấy hạng tử bậc cao nhất của A chia cho hạng tử bậc cao nhất của B. Bước 2: Lấy A trừ đi tích của B với thương mới thu được ở bước 1 Bước 3: Lấy hạng tử bậc cao nhất của dư thứ nhất chia cho hạng tử bậc cao nhất của B Bước 4: Lấy dư thứ nhất trừ đi tích B với thương vừa thu được ở bước 3 Bước 5: Làm tương tự như trên Đến khi dư cuối cùng có bậc nhỏ hơn bậc của B thì quá trình chia kết thúc. Lời giải chi tiết: a) (-x6 + 5x4 – 2x3) : (0,5x2) = (-x6 : 0,5x2) + (5x4 : 0,5x2) + (-2x3 : 0,5x2) = -2x4 + 10x2 – 4x b) Vận dụng Vận dụng giải bài toán tròn tính huống mở đầu Tìm đa thức P sao cho A = B. P, trong đó A = 2x4 – 3x3 – 3x2 + 6x – 2 và B = x2 – 2 Phương pháp giải: +) P = A : B +) Muốn chia đa thức A cho đa thức B, ta làm như sau: Bước 1: Đặt tính chia tương tự như chia hai số tự nhiên. Lấy hạng tử bậc cao nhất của A chia cho hạng tử bậc cao nhất của B. Bước 2: Lấy A trừ đi tích của B với thương mới thu được ở bước 1 Bước 3: Lấy hạng tử bậc cao nhất của dư thứ nhất chia cho hạng tử bậc cao nhất của B Bước 4: Lấy dư thứ nhất trừ đi tích B với thương vừa thu được ở bước 3 Bước 5: Làm tương tự như trên Đến khi dư cuối cùng có bậc nhỏ hơn bậc của B thì quá trình chia kết thúc. Lời giải chi tiết: Ta có: A = B . P nên P = A : B
|