Giải mục 2 trang 4, 5 SGK Toán 11 tập 2 - Cùng khám pháỞ lớp dưới, ta đã biết số (sqrt 2 ) là một số vô tỉ được biểu diễn dưới dạng số thập phân vô hạn không tuần hoàn: (sqrt 2 ) = 1,414213562...
Lựa chọn câu để xem lời giải nhanh hơn
Hoạt động 2 Tìm một số thực a cho mỗi dấu "?" trong bảng sau:
Phương pháp giải: \({a^n} = b\): Viết b dưới dạng lũy thừa số mũ n. Lời giải chi tiết:
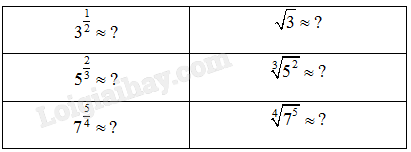
Hoạt động 3 a) Hãy dùng máy tính cầm tay để tìm kết quả cho mỗi dấu "?" (với 9 chữ số thập phân). b) Từ các kết quả ở câu a), hãy dự đoán mối quan hệ giữa hai số \({a^{\frac{m}{n}}}\) và \(\sqrt[n]{{{a^m}}}\) với a > 0 và m, n là số tự nhiên, n ≥ 2.
Phương pháp giải: a) Sử dụng máy tính cầm tay. b) So sánh kết quả giữa 2 cột. Lời giải chi tiết: a)
b) \({a^{\frac{m}{n}}}\) = \(\sqrt[n]{{{a^m}}}\) Luyện tập 2 Không dùng máy tính cầm tay, tính giá trị biểu thức \(B = {27^{\frac{2}{3}}} + {\left( {\frac{1}{{16}}} \right)^{ - 0,75}} - {25^{0,5}}\). Phương pháp giải: Áp dụng: \({\left( {{a^n}} \right)^m} = {a^{n.m}};\,{a^{ - n}} = \frac{1}{{{a^n}}}\) Lời giải chi tiết: \(\begin{array}{l}B = {27^{\frac{2}{3}}} + {\left( {\frac{1}{{16}}} \right)^{ - 0,75}} - {25^{0,5}}\\ = {\left( {{3^3}} \right)^{\frac{2}{3}}} + {\left( {{{\left( {\frac{1}{2}} \right)}^4}} \right)^{ - \frac{3}{4}}} - {\left( {{5^2}} \right)^{\frac{1}{2}}}\\ = {3^2} + {\left( {\frac{1}{2}} \right)^{ - 3}} - {5^1} = 9 + {2^3} - 5 = 12\end{array}\)
|