Giải mục 2 trang 23, 24, 25 SGK Toán 10 tập 1 - Chân trời sáng tạo

HĐ Khám phá 2

Trở lại bảng thông tin về kết quả phỏng vấn tuyển dụng ở Hoạt động khám phá 1.

a) Xác định tập hợp E gồm những ứng viên đạt yêu cầu về chuyên môn nhưng không đạt yêu cầu về ngoại ngữ.

b) Xác định tập hợp F gồm những ứng viên không đạt yêu cầu về chuyên môn.

Phương pháp giải:

Viết tập hợp bằng cách liệt kê các phần tử.

Lời giải chi tiết:

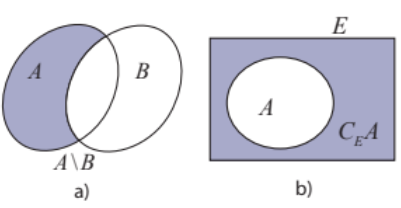
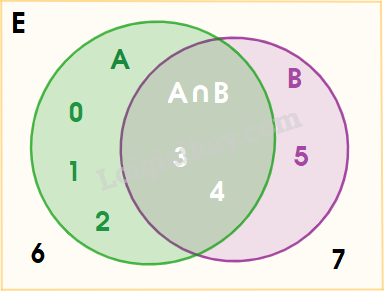
a) Tập hợp E gồm những ứng viên đạt yêu cầu về chuyên môn nhưng không đạt yêu cầu về ngoại ngữ là: $E = \{ {a_2};{a_7}\}$

b) Xác định tập hợp F gồm những ứng viên không đạt yêu cầu về chuyên môn là: $F = \{ {a_3};{a_4};{a_9}\}$

Thực hành 3

Cho tập hợp $E = \{ x \in \mathbb{N}|x < 8\} ,A = \{ 0;1;2;3;4\} ,B = \{ 3;4;5\}$

Xác định các tập hợp sau đây:

a) A\B, B\A và $(A\backslash B) \cap {\rm{(}}B\backslash A)$

b) ${C_E}(A \cap B)$ và $({C_E}A) \cap ({C_E}B)$

c) ${C_E}(A \cup B)$ và $({C_E}A) \cup ({C_E}B)$

Phương pháp giải:

Lời giải chi tiết:

$E = \{ x \in \mathbb{N}|x < 8\}  = \{ 0;1;2;3;4;5;6;7\}$

a) Ta có: $A\backslash B = \left\{ {0;1;2} \right\}$, $B\backslash A = \left\{ 5 \right\},$$(A\backslash B) \cap {\rm{(}}B\backslash A) = \emptyset$

b) Ta có: $A \cap B = \{ 3;4\} ,\;{C_E}(A \cap B) = \{ 0;1;2;5;6;7\}$

${C_E}A = \{ 5;6;7\} ,\;{C_E}B = \{ 0;1;2;6;7\}  \Rightarrow ({C_E}A) \cap ({C_E}B) = \{ 6;7\}$

c) Ta có: $A \cup B = \{ 0;1;2;3;4;5\} ,\;{C_E}(A \cup B) = \{ 6;7\}$

${C_E}A = \{ 5;6;7\} ,\;{C_E}B = \{ 0;1;2;6;7\}  \Rightarrow ({C_E}A) \cup ({C_E}B) = \{ 0;1;2;5;6;7\}$

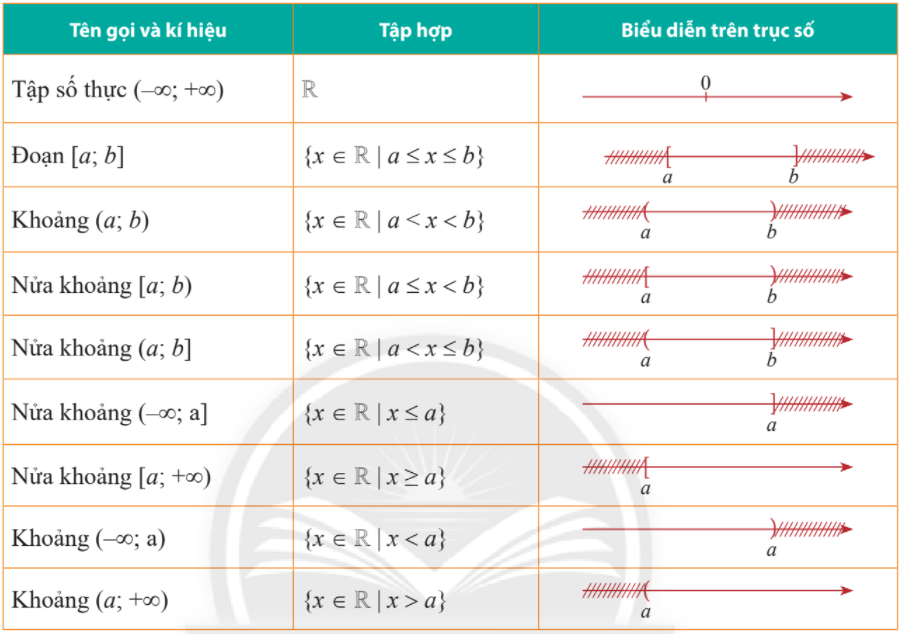
Thực hành 4

Xác định các tập hợp sau đây:

a) $(1;3) \cup [ - 2;2]$

b) $( - \infty ;1) \cap [0;\pi ]$

c) $[\frac{1}{2};3){\rm{\backslash }}(1; + \infty )$

d) ${C_\mathbb{R}}[ - 1; + \infty )$

Phương pháp giải:

Biểu diễn các tập hợp trên trục số

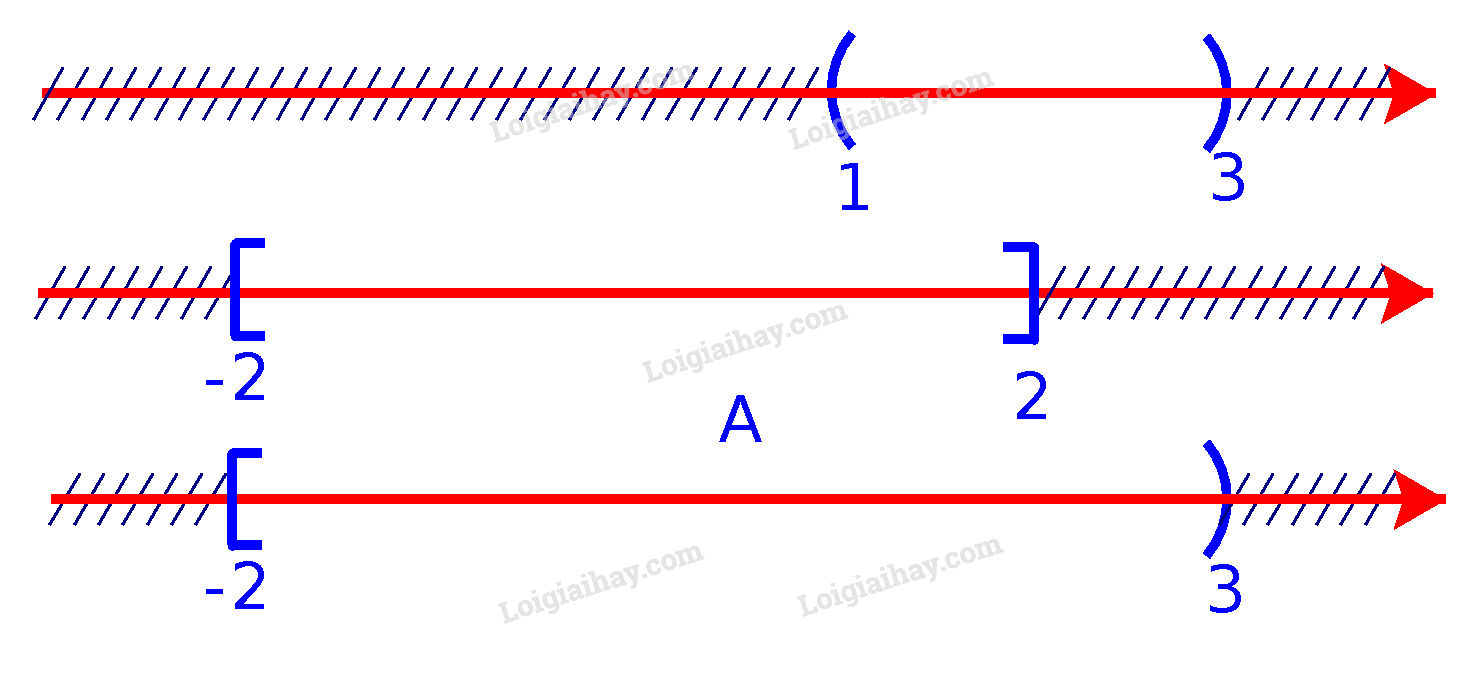
Lời giải chi tiết:

a) Để xác định tập hợp $A = (1;3) \cup [ - 2;2]$, ta vẽ sơ đồ sau đây:

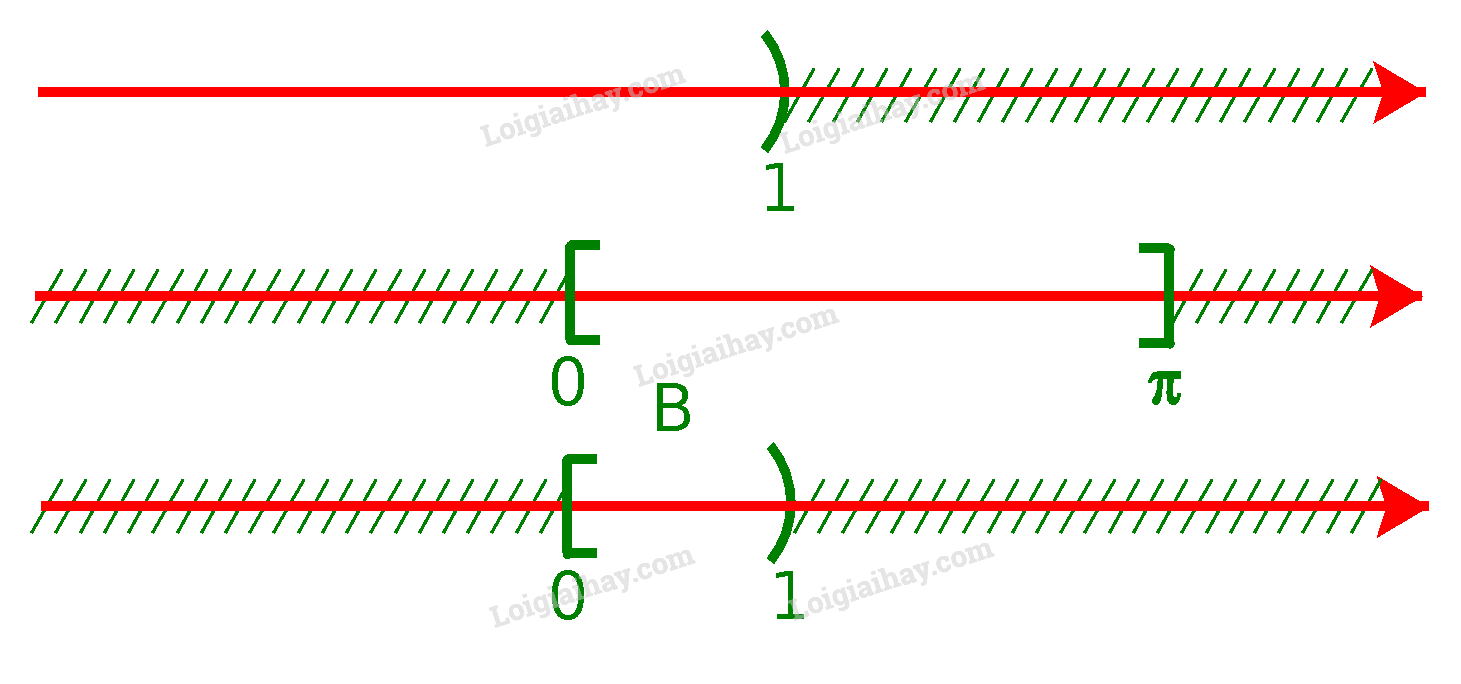
Từ sơ đồ, ta thấy $A = [ - 2;3)$

b) Để xác định tập hợp $B = ( - \infty ;1) \cap [0;\pi ]$, ta vẽ sơ đồ sau đây:

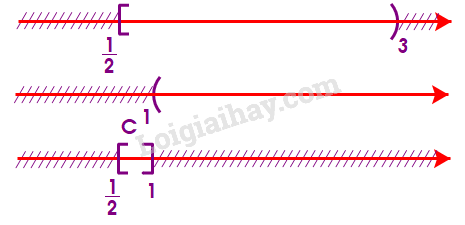
Từ sơ đồ, ta thấy $B = [0;1)$

 c) Để xác định tập hợp $C = [\frac{1}{2};3){\rm{\backslash }}(1; + \infty )$, ta vẽ sơ đồ sau đây:

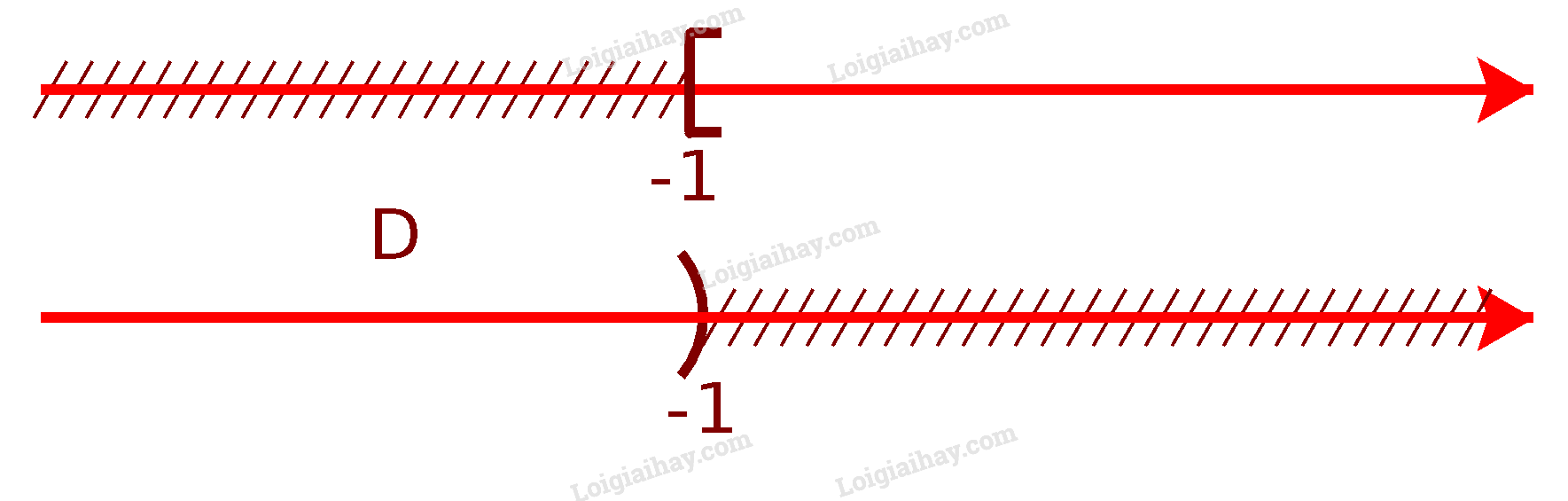
Từ sơ đồ, ta thấy $C = [\frac{1}{2};1]$

d) Để xác định tập hợp $D = {C_\mathbb{R}}[ - 1; + \infty )$, ta vẽ sơ đồ sau đây:

Từ sơ đồ, ta thấy $D = ( - \infty ; - 1)$