Giải mục 2 trang 119, 120, 121 SGK Toán 9 tập 1 - Cánh diều

HĐ3

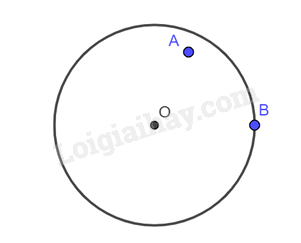
Trả lời câu hỏi Hoạt động 3 trang 119 SGK Toán 9 Cánh diều

Vẽ đường tròn $\left( {O;2cm} \right)$ và các điểm $A,B$ thỏa mãn $OA < 2cm,OB = 2cm$. Nêu nhận xét về vị trí của các điểm $A,B$ so với đường tròn $\left( {O;2cm} \right)$.

Phương pháp giải:

Dựa vào hình ảnh trực quan và các kiến thức đã học để trả lời bài toán.

Lời giải chi tiết:

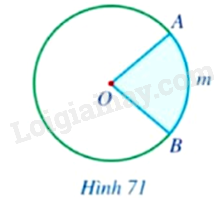
+ Điểm $A$ nằm trong đường tròn $\left( {O;2cm} \right)$.

+ Điểm $B$ nằm trên đường tròn $\left( {O;2cm} \right)$.

HĐ4

Trả lời câu hỏi Hoạt động 4 trang 120 SGK Toán 9 Cánh diều

Quan sát Hình 71, hãy cho biết phần hình tròn $\left( O \right)$ tô màu xanh được giới hạn bởi hai bán kính và cung nào?

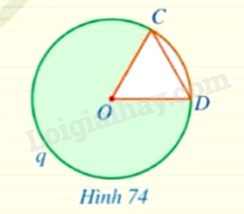
Phương pháp giải:

Dựa vào hình ảnh trực quan để nhận xét.

Lời giải chi tiết:

Phần hình tròn $\left( O \right)$ tô màu xanh được giới hạn bởi hai bán kính và cung $\overset\frown{AmB}$.

LT3

Trả lời câu hỏi Luyện tập 3 trang 120 SGK Toán 9 Cánh diều

Cho hình quạt tròn $COD$ giới hạn bởi hai bán kính $OC,OD$ và cung $CnD$ sao cho $OC = OD$ (Hình 74). Hãy tìm số đo cung $CqD$ ứng với hình quạt đó.

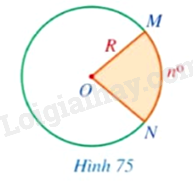
Phương pháp giải:

Chứng minh $\Delta COD$ đều nên $\widehat {COD} = {60^0}$.

Dựa vào tính chất góc ở tâm để tính số đo cung CqD.

Lời giải chi tiết:

Do OC = OD nên tam giác COD là tam giác đều, suy ra $\widehat {COD} = {60^0}$.

Vì góc COD là góc ở tâm chắn cung nhỏ CD nên sđ$\overset\frown{CD}={{60}^{o}}$.

Suy ra sđ$\overset\frown{CqD}=360^o -sđ\overset\frown{CD} = 360^o -{{60}^{o}} = 300^o$.

HĐ5

Trả lời câu hỏi Hoạt động 5 trang 120 SGK Toán 9 Cánh diều

Ta coi mỗi hình tròn bán kính $R$ là một hình quạt có số đo $360^\circ$. Tính diện tích hình quạt tròn tâm $O$, bán kính $R$, biết số đo cung ứng với hình quạt tròn đó là:

a) $1^\circ$

b) $n^\circ$ (Hình 75).

Phương pháp giải:

Dựa vào kiến thức vừa học để tính.

Lời giải chi tiết:

a) Diện tích hình tròn là: $S = \pi {R^2}$.

Diện tích hình quạt tròn tâm $O$, bán kính $R$, có số đo cung là $1^\circ$ là: $S = \frac{{\pi {R^2}}}{{360}}$.

b) Diện tích hình quạt tròn tâm $O$, bán kính $R$, có số đo cung là $n^\circ$ là: $S = \frac{{\pi {R^2}n}}{{360}}$.

LT4

Trả lời câu hỏi Luyện tập 4 trang 121 SGK Toán 9 Cánh diều

Hình quạt tô màu đỏ ở Hình 65 có bán kính bằng 2 dm và góc ở tâm bằng $150^\circ$.

a) Tính diện tích của hình quạt đó theo đơn vị decimét vuông (làm tròn kết quả đến hàng phần trăm).

b) Tính chiều dài cung tương ứng với hình quạt tròn đó.

Phương pháp giải:

Dựa vào công thức:

+ $S = \frac{{\pi {R^2}n}}{{360}}$ để tính diện tích của hình quạt.

+ $l = \frac{{\pi Rn}}{{180}}$ để tính chiều dài cung tương ứng.

Lời giải chi tiết:

a) Diện tích của hình quạt đó là:

$S = \frac{{\pi .{2^2}.150}}{{360}} \approx 5,24\left( {d{m^2}} \right)$.

b) Chiều dài cung tương ứng với hình quạt tròn đó là:

$l = \frac{{\pi Rn}}{{180}} = \frac{{\pi .2.150}}{{180}} = \frac{{5\pi }}{3}\left( {dm} \right)$.