Giải mục 2 trang 108, 109 SGK Toán 11 tập 1 - Chân trời sáng tạo

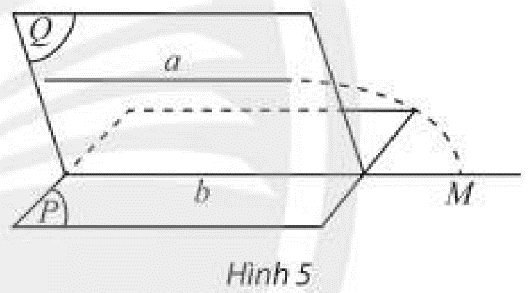
Hoạt động 2

Cho đường thẳng $a$ không nằm trong mặt phẳng $\left( P \right)$ và $a$ song song với một đường thẳng $b$ nằm trong $\left( P \right)$. Đặt $\left( Q \right) = mp\left( {a,b} \right)$.

a) Tìm giao tuyến của hai mặt phẳng $\left( P \right)$ và $\left( Q \right)$.

b) Giả sử $a$ có điểm chung $M$ với $\left( P \right)$ thì điểm $M$ phải nằm trên đường thẳng nào? Điều này có trái với giả thiết $a\parallel b$ hay không?

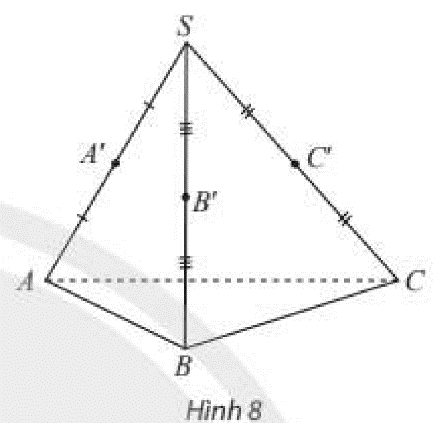
Phương pháp giải:

‒ Để tìm giao tuyến của hai mặt phẳng, ta tìm hai điểm chung phân biệt hoặc một đường thẳng chung của hai mặt phẳng.

‒ Để tìm vị trí của điểm $M$, ta sử dụng tính chất về giao tuyến của hai mặt phẳng.

Lời giải chi tiết:

a) Ta có:

$\left. \begin{array}{l}b \subset \left( P \right)\\b \subset \left( Q \right)\end{array} \right\} \Rightarrow b = \left( P \right) \cap \left( Q \right)$

Vậy $b$ là giao tuyến của hai mặt phẳng $\left( P \right)$ và $\left( Q \right)$.

b) Ta có:

$\left. \begin{array}{l}M \in a\\a \subset \left( Q \right)\end{array} \right\} \Rightarrow M \in \left( Q \right)$

Lại có: $M \in \left( P \right)$

Do đó điểm $M$ nằm trên giao tuyến của hai mặt phẳng $\left( P \right)$ và $\left( Q \right)$. Vậy $M \in b$.

Vậy $M$ là một điểm chung của hai đường thẳng $a$ và $b$, trái với giả thiết $a\parallel b$.

Quảng cáo

Thực hành 2

Cho hình chóp $S.ABC$ có $A',B',C'$ lần lượt là trung điểm của $SA,SB,SC$. Tìm các đường thẳng lần lượt nằm trong, cắt, song song với mặt phẳng $\left( {ABC} \right)$.

Phương pháp giải:

‒ Để xác định vị trí tương đối của đường thẳng và mặt phẳng, ta dựa vào số điểm chung của đường thẳng và mặt phẳng đó.

‒ Để xác định đường thẳng song song với mặt phẳng, ta sử dụng định lí 1: Nếu đường thẳng $a$ không nằm trong mặt phẳng $\left( P \right)$ và song song với một đường thẳng $b$ nào đó nằm trong $\left( P \right)$ thì $a$ song song với $\left( P \right)$.

Lời giải chi tiết:

$\begin{array}{l}\left. \begin{array}{l}A \in \left( {ABC} \right)\\B \in \left( {ABC} \right)\end{array} \right\} \Rightarrow AB \subset \left( {ABC} \right)\\\left. \begin{array}{l}B \in \left( {ABC} \right)\\C \in \left( {ABC} \right)\end{array} \right\} \Rightarrow BC \subset \left( {ABC} \right)\\\left. \begin{array}{l}A \in \left( {ABC} \right)\\C \in \left( {ABC} \right)\end{array} \right\} \Rightarrow AC \subset \left( {ABC} \right)\end{array}$

$SA \cap \left( {ABC} \right) = \left\{ A \right\} \Rightarrow SA$ cắt mặt phẳng $\left( {ABC} \right)$.

$SB \cap \left( {ABC} \right) = \left\{ B \right\} \Rightarrow SB$ cắt mặt phẳng $\left( {ABC} \right)$.

$SC \cap \left( {ABC} \right) = \left\{ C \right\} \Rightarrow SC$ cắt mặt phẳng $\left( {ABC} \right)$.

$A'B \cap \left( {ABC} \right) = \left\{ B \right\} \Rightarrow A'B$ cắt mặt phẳng $\left( {ABC} \right)$.

$A'C \cap \left( {ABC} \right) = \left\{ C \right\} \Rightarrow A'C$ cắt mặt phẳng $\left( {ABC} \right)$.

$B'A \cap \left( {ABC} \right) = \left\{ A \right\} \Rightarrow B'A$ cắt mặt phẳng $\left( {ABC} \right)$.

$B'C \cap \left( {ABC} \right) = \left\{ C \right\} \Rightarrow B'C$ cắt mặt phẳng $\left( {ABC} \right)$.

$C'A \cap \left( {ABC} \right) = \left\{ A \right\} \Rightarrow C'A$ cắt mặt phẳng $\left( {ABC} \right)$.

$C'B \cap \left( {ABC} \right) = \left\{ B \right\} \Rightarrow C'B$ cắt mặt phẳng $\left( {ABC} \right)$.

$A'$ là trung điểm của $SA$

$B'$ là trung điểm của $SB$

$\Rightarrow A'B'$ là đường trung bình của tam giác $SAB$

$\left. \begin{array}{l} \Rightarrow A'B'\parallel AB\\AB \subset \left( {ABC} \right)\end{array} \right\} \Rightarrow A'B'\parallel \left( {ABC} \right)$

$A'$ là trung điểm của $SA$

$C'$ là trung điểm của $SC$

$\Rightarrow A'C'$ là đường trung bình của tam giác $SAC$

$\left. \begin{array}{l} \Rightarrow A'C'\parallel AC\\AC \subset \left( {ABC} \right)\end{array} \right\} \Rightarrow A'C'\parallel \left( {ABC} \right)$

$B'$ là trung điểm của $SB$

$C'$ là trung điểm của $SC$

$\Rightarrow B'C'$ là đường trung bình của tam giác $SBC$

$\left. \begin{array}{l} \Rightarrow B'C'\parallel BC\\BC \subset \left( {ABC} \right)\end{array} \right\} \Rightarrow B'C'\parallel \left( {ABC} \right)$

Thực hành 3

Hãy chỉ ra trong Hình 9 các đường thẳng lần lượt nằm trong, song song, cắt mặt phẳng sàn nhà.

Phương pháp giải:

Để xác định vị trí tương đối của đường thẳng và mặt phẳng, ta dựa vào số điểm chung của đường thẳng và mặt phẳng đó.

Lời giải chi tiết:

Các đường thẳng nằm trong mặt phẳng sàn nhà là: mép chân giường, chân tường, mép chân bàn, viền thảm trải sàn,…

Các đường thẳng song song với mặt phẳng sàn nhà là: mép cạnh bàn, mép kệ, mép trần nhà, mép cửa sổ,…

Các đường thẳng cắt mặt phẳng sàn nhà là: cạnh tường, cạnh thẳng đứng của kệ, tủ,…