Giải mục 1 trang 73, 74, 75, 76 SGK Toán 8 tập 1– Chân trời sáng tạoHình 1a là hình ảnh của một thước vẽ truyền Tổng hợp đề thi học kì 1 lớp 8 tất cả các môn - Chân trời sáng tạo Toán - Văn - Anh - Khoa học tự nhiên
Lựa chọn câu để xem lời giải nhanh hơn
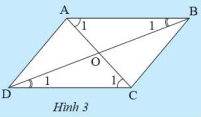
HĐ 1 Video hướng dẫn giải Hình 1a là hình ảnh của một thước vẽ truyền dùng để phóng to hay thu nhỏ một hình vẽ có sẵn. Dùng thước đo góc để đo số đo của các cặp góc \(\widehat {{A_1}}\) và \(\widehat {\rm{D}}\), \(\widehat {{{\rm{C}}_{\rm{1}}}}\) và \(\widehat {\rm{D}}\) của tứ giác \(ABCD\) (Hình 1b) rồi rút ra nhận xét về mối quan hệ giữa các cặp cạnh \(AB\) và \(CD\); \(AD\) và \(BC\).
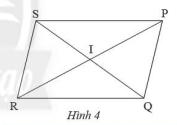
Phương pháp giải: Sử dụng thước đo góc đo số đo các góc theo yêu cầu Sử dụng kiến thức chỉ ra các cặp đường thẳng song song Lời giải chi tiết: Sau khi đo góc ta thấy cặp góc \(\widehat {{A_1}}\) và \(\widehat {\rm{D}}\), \(\widehat {{{\rm{C}}_{\rm{1}}}}\) và \(\widehat {\rm{D}}\) bằng nhau Mà các góc ở vị trí đồng vị Suy ra: \(AB\) // \(CD\); \(AD\) // \(BC\) HĐ 2 Video hướng dẫn giải Cho tứ giác \(ABCD\) có các cạnh đối song song. Gọi \(O\) là giao điểm của hai đường chéo. Hãy chứng tỏ: - Tam giác \(ABC\) bằng tam giác \(CDA\) - Tam giác \(OAB\) bằng tam giác \(OCD\)
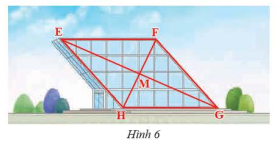
Phương pháp giải: Áp dụng tính chất của hai đường thẳng song song Áp dụng trường hợp bằng nhau thứ 2 của tam giác Lời giải chi tiết: Xét \(\Delta ABC\) và \(\Delta CDA\) ta có: \(\widehat {{{\rm{A}}_{\rm{1}}}} = \widehat {{{\rm{C}}_{\rm{1}}}}\) (do \(AB\) // \(CD\)) \(AC\) chung \(\widehat {{\rm{ACB}}} = \widehat {{\rm{CAD}}}\) (do \(AD\) // \(BC\)) Suy ra: \(\Delta ABC = \Delta CDA\) (c-g-c) Xét \(\Delta OAB\) và \(\Delta OCD\) ta có: \(\widehat {{{\rm{A}}_{\rm{1}}}} = \widehat {{{\rm{C}}_{\rm{1}}}}\) (do \(AB\) // \(CD\)) AB = CD (do \(\Delta ABC = \Delta CDA\)) \(\widehat {{{\rm{B}}_{\rm{1}}}} = \widehat {{{\rm{D}}_{\rm{1}}}}\) (do \(\Delta ABC = \Delta CDA\)) Suy ra: \(\Delta OAB = \Delta OCD\) (g-c-g) TH 1 Video hướng dẫn giải Cho hình bình hành \(PQRS\) với \(I\) là giao điểm của hai đường chéo (Hình 4). Hãy chỉ ra các đoạn thẳng bằng nhau và các góc bằng nhau có trong hình.
Phương pháp giải: Áp dụng tính chất của hình bình hành Lời giải chi tiết: Trong hình bình hành \(PQRS\) với \(I\) là giao điểm của hai đường chéo, ta có: \(IS = IQ\); \(IP = IR\); \(PS = QR\); \(SR = PQ\) \(\widehat {{\rm{RSP}}} = \widehat {{\rm{RQP}}}\); \(\widehat {{\rm{SRQ}}} = \widehat {{\rm{SPQ}}}\) VD 1 Video hướng dẫn giải Mắt lưới của một lưới bóng chuyền có dạng hình tứ giác có các cạnh đối song song. Cho biết độ dài hai cạnh của tứ giác này là 4cm và 5cm. Tìm độ dài hai cạnh còn lại. Phương pháp giải: Áp dụng tính chất của hình bình hành Lời giải chi tiết: Mắt lướt bóng chuyền có các cạnh đối song song nên mắt lưới có dạng hình bình hành Vậy độ dài hai cạnh còn lại lần lượt bằng 4cm và 5cm VD 2 Video hướng dẫn giải Mặt trước của một công trình xây dựng được làm bằng kính có dạng hình bình hành \(EFGH\) với \(M\) là giao điểm của hai đường chéo (Hình 6). Cho biết \(EF = 40\)m, \(EM = 36\)m, \(HM = 16\)m. Tính độ dài cạnh \(HG\) và độ dài hai đường chéo.
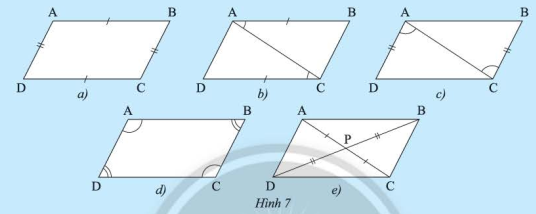
Phương pháp giải: Sử dụng tính chất hình hình hành để tính các cạnh theo yêu cầu Lời giải chi tiết: Vì \(EFGH\) là hình bình hành Suy ra: \(EF = HG = 40\)m; \(EM = MG = 36\)m; \(HM = MF = 16\)m Suy ra: \(EG = 72\)m; \(HF = 32\)m HĐ 3 Video hướng dẫn giải Cho tứ giác \(ABCD\) có \(P\) là giao điểm của hai đường chéo. Giải thích tại sao \(AB\) // \(CD\) và \(AD\) // \(BC\) trong mỗi trường hợp sau: Trường hợp 1: \(AB = CD\) và \(AD = BC\) (Hình 7a) Trường hợp 2: \(AB\) // \(CD\) và \(AB = CD\) (Hình 7b) Trường hợp 3: \(AD\) // \(BC\) và \(AD = BC\) (Hình 7c) Trường hợp 4: \(\widehat {\rm{A}} = \widehat {\rm{C}}\), \(\widehat {\rm{B}} = \widehat {\rm{D}}\) (Hình 7d) Trường hợp 5: \(PA = PC\), \(PB = PD\) (Hình 7e)
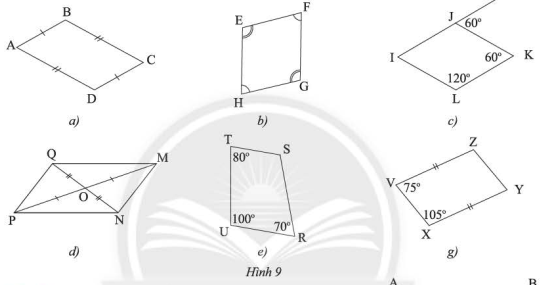
Phương pháp giải: Chứng minh các góc ở vị trí trong cùng phía bù nhau, so le trong bằng nhau Lời giải chi tiết: a) Xét \(\Delta ABC\) và \(\Delta CDA\) ta có: \(AB = CD\) (gt) \(AD = BC\) (gt) \(AC\) chung Suy ra: \(\Delta ABC = \Delta CDA\) (c-c-c) \( \Rightarrow \widehat {BAC} = \widehat {ACD}\) (hai góc tương ứng) Mà hai góc ở vị trí so le trong Suy ra \(AB\) // \(CD\) Chứng minh tương tự \(\Delta ADB = \Delta CBD\) (c-c-c) \( \Rightarrow \widehat {ABD} = \widehat {CDB}\) (hai góc tương ứng) Mà hai góc ở vị trí so le trong b) Xét \(\Delta ABC\) và \(\Delta CDA\) ta có: \(AB = CD\) (gt) \(\widehat {{\rm{BAC}}} = \widehat {{\rm{ACD}}}\) (do \(AB\) // \(CD\)) \(AC\) chung Suy ra: \(\Delta ABC = \Delta CDA\) (c-g-c) \( \Rightarrow \widehat {BCA} = \widehat {CAD}\) (hai góc tương ứng) Mà hai góc ở vị trí so le trong Suy ra \(AD\;{\rm{//}}\;BC\) c) Xét \(\Delta ABC\) và \(\Delta CDA\) ta có: \(BC = AD\) (gt) \(\widehat {{\rm{BCA}}} = \widehat {{\rm{CDA}}}\) (do \(AD\) // \(BC\)) \(AC\) chung Suy ra \(\Delta ABC = \Delta CDA\) (c-g-c) Suy ra \(\widehat {{\rm{BAC}}} = \widehat {{\rm{ACD}}}\) (hai góc tương ứng) Mà hai góc ở vị trí so le trong Suy ra: \(AB\) // \(CD\) d) Xét tứ giác \(ABCD\) ta có: \(\widehat A + \widehat B + \widehat C + \widehat D = 360^\circ \) Mà \(\widehat A = \widehat C\); \(\widehat B = \widehat D\) (gt) Suy ra \(\widehat A + \widehat D = 180^\circ ;\;\widehat A + \widehat B = 180^\circ \) Mà hai góc ở vị trí trong cùng phía Suy ra \(AB\;{\rm{//}}\;CD;\;AD\;{\rm{//}}\;BC\) e) Xét \(\Delta APB\) và \(\Delta CPD\) ta có: \(PA = PC\) (gt) \(\widehat {{\rm{APB}}} = \widehat {{\rm{CPD}}}\) (đối đỉnh) \(PB = PD\) (gt) Suy ra: \(\Delta APB = \Delta CPD\) (c-g-c) Suy ra: \(\widehat {BAP} = \widehat {PCD}\) (hai góc tương ứng) Mà hai góc ở vị trí so le trong Suy ra \(AB\;{\rm{//}}\;CD\) Chứng minh tương tự: \(\Delta APD = \Delta CPB\) (c-g-c) Suy ra \(\widehat {{\rm{DAP}}} = \widehat {{\rm{BCP}}}\) (hai góc tương ứng) Mà hai góc ở vị trí so le trong Suy ra \(AD\) // \(BC\) TH 2 Video hướng dẫn giải Trong các tứ giác ở Hình 9, tứ giác nào không là hình bình hành?
Phương pháp giải: Sử dụng dấu hiệu nhận biết hình bình hành Lời giải chi tiết: a) Xét tứ giác \(ABCD\) ta có: \(AB = CD\) (gt) \(AD = BC\) (gt) Suy ra: \(ABCD\) là hình bình hành b) Xét tứ giác \(EFGH\) ta có: \(\widehat {\rm{E}} = \widehat G\) (gt) \(\widehat F = \widehat H\) (gt) Suy ra \(EFGH\) là hình bình hành c) Ta có: \(\widehat J = \widehat {\rm{K}} = 60^\circ \) (gt) Mà hai góc ở vị trí so le trong Suy ra \(IJ\) // \(KL\) (1) Ta có: \(\widehat K + \widehat L = 60^\circ + 120^\circ = 180^\circ \) Mà hai góc ở vị trí trong cùng phía Suy ra \(JK\;{\rm{//}}\;IL\) (2) Từ (1), (2) suy ra \(IJKL\) là hình bình hành d) Xét tứ giác \(MNPQ\) ta có: \(O\) là trung điểm của \(NQ\) (do \(OQ = ON\)) \(O\) là trung điểm của \(MP\) (do \(OP = OM\)) Suy ra \(MNPQ\) là hình bình hành e) Tứ giác \(TSRU\) không là hình bình hành g) Ta có: \(\widehat {\rm{V}} + \widehat {\rm{X}} = 75^\circ + 105^\circ = 180^\circ \) Mà hai góc ở vị trí trong cùng phía Suy ra: \(VZ\) // \(XY\) Xét tứ giác \(VZYX\) ta có: \(VZ\) // \(XY\) (cmt) \(VZ = XY\) (gt) Suy ra \(VZYX\) là hình bình hành VD 3 Video hướng dẫn giải Quan sát Hình 10, cho biết \(ABCD\) và \(AKCD\) đều là hình bình hành. Chứng minh ba đoạn thẳng \(AC\), \(BD\) và \(HK\) có cùng trung điểm \(O\).
Phương pháp giải: Sử dụng tính chất của hình bình hành Lời giải chi tiết: Vì \(ABCD\) là hình bình hành (gt) Suy ra \(O\) là trung điểm của \(AC\) và \(BD\) (1) Vì \(AKCH\) là hình bình hành (gt) Mà \(O\) là trung điểm của \(AC\) Suy ra \(O\) là trung điểm của \(HK\)
|