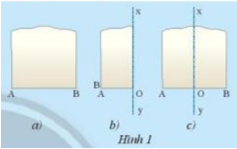
Giải mục 1 trang 67 SGK Toán 7 tập 2 - Chân trời sáng tạoLấy một mảnh giấy như trong Hình 1a, gọi một mép cắt là đoạn thẳng AB. Sau đó gấp mảnh giấy sao cho điểm A trùng với điểm B (Hình 1b) Theo em nếp gấp xy có vuông góc với đoạn AB tại trung điểm hay không? Tại sao? Video hướng dẫn giải HĐ 1 Lấy một mảnh giấy như trong Hình 1a, gọi một mép cắt là đoạn thẳng AB. Sau đó gấp mảnh giấy sao cho điểm A trùng với điểm B (Hình 1b) Theo em nếp gấp xy có vuông góc với đoạn AB tại trung điểm hay không? Tại sao?
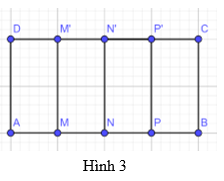
Phương pháp giải: - Gấp theo hướng dẫn Lời giải chi tiết: Sau khi gấp A trùng với B thì điểm gấp trên cạnh AB là O ⇒⇒ AO = BO ⇒⇒O là trung điểm AB Vì 2 mép của tờ giấy song song với nhau nên khi gấp đôi đường gấp ở giữa (xy) cũng song song với 2 cạnh của tờ giấy . Mà 2 cạnh của tờ giấy vuông góc với AB nên xy cũng vuông góc với AB Thực hành 1 Cho hình chữ nhật ABCD, trên cạnh AB lấy các điểm M, N, P và trên cạnh DC lấy các điểm M’, N’, P’. Cho biết AM = MN = NP = PB và MM’, NN’, PP’ đều song song với BC (Hình 3). Tìm đường trung trực của mỗi đoạn thẳng AB, AN và NB.
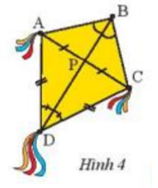
Phương pháp giải: - Dựa vào định nghĩa của đường trung trực Lời giải chi tiết: Đường trung trực của AB là NN’ vì NN' vuông góc với AB tại trung điểm N của AB. Đường trung trực của AN là MM’ vì MM' vuông góc với AN tại trung điểm M của AN. Đường trung trực của NB là PP’ vì PP' vuông góc với NB tại trung điểm P của NB. Vận dụng 1 Trong Hình 4, hãy cho biết BD có là đường trung trực của đoạn thẳng AC hay không? Tại sao?
Phương pháp giải: - Chứng minh P là trung điểm AC - Chứng minh BD vuông góc với AC Lời giải chi tiết: Theo giả thiết ta có P là trung điểm AC Xét tam giác APD và tam giác CPD có : AP = PC ( theo giả thiết ) DP cạnh chung AD = CD ( theo giả thiết ) Suy ra tΔAPD=ΔCPD(c−c−c)ΔAPD=ΔCPD(c−c−c) ⇒^CPD=^APD⇒ˆCPD=ˆAPD (2 góc tương ứng ) Mà 2 góc ở vị trí kề bù ⇒^CPD=^APD=90o⇒ˆCPD=ˆAPD=90o⇒AC⊥BD⇒AC⊥BD và P là chung điểm AC do AP = PC ⇒⇒ BD là đường trung trực của AC
|