Giải mục 1 trang 56, 57, 58 Chuyên đề học tập Toán 10 - Chân trời sáng tạoChứng tỏ rằng nếu điểm \(M({x_0};{y_0})\) nằm trên parabol (P) thì điểm \(N({x_0}; - {y_0})\) cũng nằm trên parabol (P) Tổng hợp đề thi học kì 2 lớp 10 tất cả các môn - Chân trời sáng tạo Toán - Văn - Anh - Lí - Hóa - Sinh - Sử - Địa...
Lựa chọn câu để xem lời giải nhanh hơn
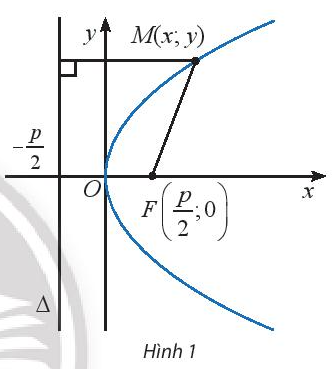
HĐ1 Chứng tỏ rằng nếu điểm \(M({x_0};{y_0})\) nằm trên parabol (P) thì điểm \(N({x_0}; - {y_0})\) cũng nằm trên parabol (P)
Lời giải chi tiết: Nếu điểm \(M({x_0};{y_0})\) nằm trên parabol thì \({y_0}^2 = 2p{x_0} \Leftrightarrow {( - {y_0})^2} = 2p{x_0}\) nên điểm \(M'({x_0}; - {y_0})\) cũng nằm trên parabol. Thực hành 1 Tìm tọa độ tiêu điểm, tọa độ đỉnh, phương trình đường chuẩn và trục đối xứng của các parabol sau: a) \(({P_1}):{y^2} = 2x\) b) \(({P_2}):{y^2} = x\) c) \(({P_3}):{y^2} = \frac{1}{5}x\) Phương pháp giải: Cho parabol có PTCT \({y^2} = 2px\) + Tiêu điểm: \(F\left( {\frac{p}{2};0} \right)\) + Đỉnh O(0;0) + Đường chuẩn: \(\Delta :x = - \frac{p}{2}\) + Trục đối xứng: Ox Lời giải chi tiết: a) Ta có: \(2p = 2\), suy ra \(p = 1\). Vậy \(({P_1})\) có tiêu điểm \(F\left( {\frac{1}{2};0} \right)\), đỉnh \(O(0;0)\), đường chuẩn \(\Delta :x = - \frac{1}{2}\) và nhận Ox làm trục đối xứng. b) Ta có: \(2p = 1\), suy ra \(p = \frac{1}{2}\). Vậy \(({P_2})\) có tiêu điểm \(F\left( {\frac{1}{4};0} \right)\), đỉnh \(O(0;0)\), đường chuẩn \(\Delta :x = - \frac{1}{4}\) và nhận Ox làm trục đối xứng. c) Ta có: \(2p = \frac{1}{5}\), suy ra \(p = \frac{1}{{10}}\). Vậy \(({P_2})\) có tiêu điểm \(F\left( {\frac{1}{{20}};0} \right)\), đỉnh \(O(0;0)\), đường chuẩn \(\Delta :x = - \frac{1}{{20}}\) và nhận Ox làm trục đối xứng.
Vận dụng 1 Trong mặt phẳng Oxy, cho điểm \(A(2;0)\) và đường thẳng \(d:x + 2 = 0\). Viết phương trình của đường (L) là tập hợp các tâm \(J(x;y)\) của các đường tròn (C) thay đổi nhưng luôn luôn đi qua A và tiếp xúc với d. Lời giải chi tiết: Ta có: (C) đi qua \(A(2;0)\) và tiếp xúc với \(d:x + 2 = 0\) \(\begin{array}{l} \Rightarrow d(J,d) = JA\\ \Leftrightarrow \left| {x + 2} \right| = \sqrt {{{(x - 2)}^2} + {y^2}} \\ \Leftrightarrow {\left( {x + 2} \right)^2} = {(x - 2)^2} + {y^2}\\ \Leftrightarrow {x^2} + 4x + 4 = {x^2} - 4x + 4 + {y^2}\\ \Leftrightarrow {y^2} = 8x\end{array}\) Tức là tâm \(J(x;y)\) của (C) nằm trên parabol (P) \({y^2} = 8x\)
>> Học trực tuyến Lớp 10 cùng thầy cô giáo giỏi tại Tuyensinh247.com, (Xem ngay) Cam kết giúp học sinh học tốt, bứt phá điểm 9,10 chỉ sau 3 tháng, làm quen kiến thức, định hướng luyện thi TN THPT, ĐGNL, ĐGTD ngay từ lớp 10
|