Giải mục 1 trang 54, 55 SGK Toán 11 tập 2 - Kết nối tri thứca) Cho điểm M và đường thẳng a. Gọi H là hình chiếu của M trên a. Với mỗi điểm K thuộc a, vì sao MK ≥ MH (H.7.74) Tổng hợp đề thi học kì 2 lớp 11 tất cả các môn - Kết nối tri thức Toán - Văn - Anh - Lí - Hóa - Sinh
Lựa chọn câu để xem lời giải nhanh hơn
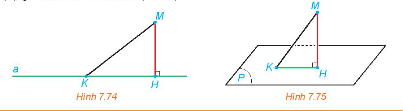
HĐ 1 Video hướng dẫn giải a) Cho điểm M và đường thẳng a. Gọi H là hình chiếu của M trên a. Với mỗi điểm K thuộc a, vì sao MK ≥ MH (H.7.74) b) Cho điểm M và mặt phẳng (P). Gọi H là hình chiếu của M trên (P). Với mỗi điểm K thuộc (P), giải thích vì sao MK ≥ MH (H.7.75).
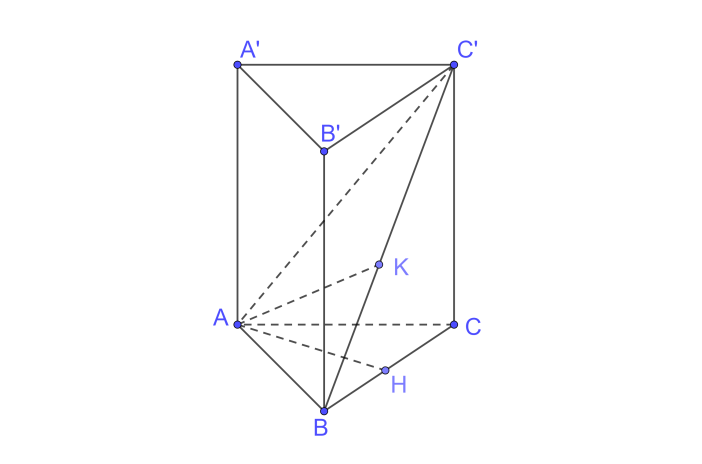
Phương pháp giải: Dựa vào mối quan hệ đường xiên và đường vuông góc. Lời giải chi tiết: a) Vì H là hình chiếu của M trên đường thẳng a, nên MH là khoảng cách từ M đến a và MH là đoạn thẳng ngắn nhất từ M đến a, suy ra MK ≥ MH. b) Vì H là hình chiếu của M trên (P) nên MH vuông góc với (P) do đó MH vuông góc với HK. Dựa vào mối quan hệ đường xiên và đường vuông góc ta có MK ≥ MH. LT 1 Video hướng dẫn giải Cho hình lăng trụ đứng ABC.A'B'C' có ABC là tam giác vuông cân tại A, AB = a, AA' = h (H.7.77). a) Tính khoảng cách từ A đến mặt phẳng (BCC'B'). b) Tam giác ABC' là tam giác gì? Tính khoảng cách từ A đến BC'.
Phương pháp giải: - Khoảng cách từ một điểm M đến một đường thẳng a, kí hiệu d (M, a), là khoảng cách giữa M và hình chiếu H của M trên a. - Khoảng cách từ một điểm M đến một mặt phẳng (P), kí hiệu d (M, (P)), là khoảng cách giữa M và hình chiếu H của M trên (P). Lời giải chi tiết:
a) Ta có BB′⊥(ABC);BB′⊂(BCC′B′)⇒(ABC)⊥(BCC′B′) (ABC)∩(BCC′B′)=BC (ABC): Kẻ AH⊥BC ⇒AH⊥(BCC′B′)⇒d(A,(BCC′B′))=AH Xét tam giác ABC vuông cân tại A có 1AH2=1AB2+1AC2=2a2 (hệ thức lượng trong tam giác vuông) ⇒AH=a√22 b) +) Ta có AB⊥AC,AB⊥AA′(AA′⊥(ABC))⇒AB⊥(ACC′A′);AC′⊂(ACC′A′)⇒AC′⊥AB Do đó tam giác ABC' là tam giác vuông. +) Trên (ABC’) kẻ AK⊥BC′⇒d(A,BC′)=AK Xét tam giác ACC’ vuông tại C có AC′2=AC2+CC′2=a2+h2 (Định lí Pytago) Xét tam giác ABC’ vuông tại A có 1AK2=1AB2+1AC′2=1a2+1a2+h2=2a2+h2a2(a2+h2)⇒AK2=a2(a2+h2)2a2+h2⇒AK=a.√a2+h22a2+h2
>> 2K8 Chú ý! Lộ Trình Sun 2026 - 3IN1 - 1 lộ trình ôn 3 kì thi (Luyện thi 26+TN THPT, 90+ ĐGNL HN, 900+ ĐGNL HCM; 70+ ĐGTD - Click xem ngay) tại Tuyensinh247.com.Đầy đủ theo 3 đầu sách, Thầy Cô giáo giỏi, 3 bước chi tiết: Nền tảng lớp 12; Luyện thi chuyên sâu; Luyện đề đủ dạng đáp ứng mọi kì thi.
|