Giải mục 3 trang 57, 58 SGK Toán 11 tập 2 - Kết nối tri thứcCho hai đường thẳng chéo nhau a và b. Tổng hợp đề thi học kì 2 lớp 11 tất cả các môn - Kết nối tri thức Toán - Văn - Anh - Lí - Hóa - Sinh
Lựa chọn câu để xem lời giải nhanh hơn
HĐ 4 Video hướng dẫn giải Cho hai đường thẳng chéo nhau a và b. Gọi (Q) là mặt phẳng chứa đường thẳng b và song song với a. Hình chiếu a' của a trên (Q) cắt b tại N. Gọi M là hình chiếu của N trên a (H.7.83).
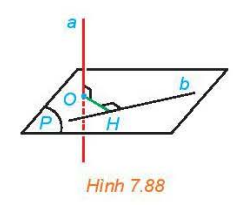
a) Mặt phẳng chứa a và a' có vuông góc với (Q) hay không? b) Đường thẳng MN có vuông góc với cả hai đường thẳng a và b hay không? c) Nêu mối quan hệ của khoảng cách giữa a, (Q) và độ dài đoạn thẳng MN. Phương pháp giải: Khoảng cách giữa đường thẳng a và mặt phẳng (P) song song với a là khoảng cách từ một điểm bất kì trên a đến (P). Lời giải chi tiết: a) Mặt phẳng chứa a và a' có vuông góc với (Q) b) Ta có MN⊥(Q),b⊂(Q)⇒MN⊥b MN⊥a (M là hình chiếu của N trên a) Vậy MN có vuông góc với cả hai đường thẳng a và b. c) Vì a // (Q) nên d(a, (Q)) = d(M, (Q)) = MN KP Video hướng dẫn giải Cho đường thẳng a vuông góc với mặt phẳng (P) và cắt (P) tại O. Cho đường thẳng b thuộc mặt phẳng (P). Hãy tìm mối quan hệ giữa khoảng cách giữa a, b và khoảng cách từ O đến b (H.7.88).
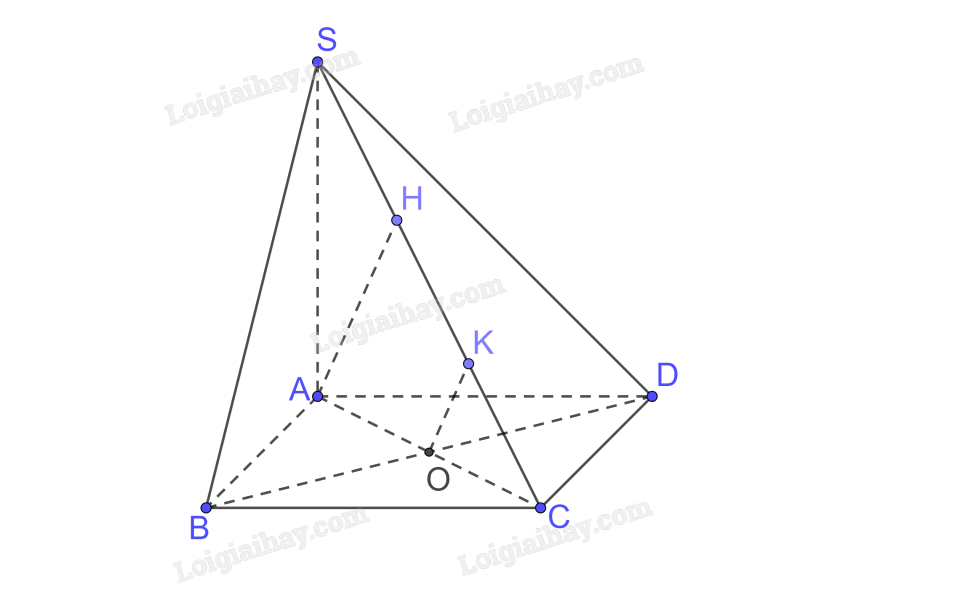
Phương pháp giải: Nếu đường vuông góc chung Δ cắt a, b tương ứng tại M, N thì độ dài đoạn thẳng MN được gọi là khoảng cách giữa hai đường thẳng chéo nhau a, b. Lời giải chi tiết: Vì a⊥(P) tại O, OH⊂(P)⇒a⊥OHtại O OH⊥b tại H ⇒d(a,b)=OH LT 3 Video hướng dẫn giải Cho hình chóp S.ABCD có đáy là hình vuông cạnh a, SA⊥(ABCD),SA=a√2. a) Tính khoảng cách từ A đến SC. b) Chứng minh BD⊥(SAC). c) Xác định đường vuông góc chung và tính khoảng cách giữa BD và SC. Phương pháp giải: - Khoảng cách từ một điểm M đến một đường thẳng a là khoảng cách giữa M và hình chiếu H của M trên a. - Đường thẳng vuông góc với mặt phẳng nếu nó vuông góc với hai đường thẳng cắt nhau nằm trong mặt phẳng đó. - Nếu đường vuông góc chung Δ cắt a, b tương ứng tại M, N thì độ dài đoạn thẳng MN được gọi là khoảng cách giữa hai đường thẳng chéo nhau a, b. Lời giải chi tiết: a) Trong (SAC) kẻ AH⊥SC⇒d(A,SC)=AH Xét tam giác ABC vuông tại B có AC=√AB2+BC2=√a2+a2=a√2 Xét ta giác SAC vuông tại A có 1AH2=1SA2+1AC2=1(a√2)2+1(a√2)2=1a2⇒AH=a ⇒d(A,SC)=a b) Ta có BD⊥AC,BD⊥SA(SA⊥(ABCD))⇒BD⊥(SAC) c) Trong (SAC) kẻ OK⊥SC OK⊥BD(BD⊥(SAC))⇒d(SC,BD)=OK Xét tam giác AHC vuông tại H có O là trung điểm AC OK // AH (cùng vuông góc SC) ⇒ OK là đường trung bình ⇒ OK=12AH=a2⇒d(BD,SC)=a2 TL Video hướng dẫn giải Khoảng cách giữa hai hình được nêu trong bài học (điểm, đường thẳng, mặt phẳng) là khoảng cách nhỏ nhất giữa một điểm thuộc hình này và một điểm thuộc hình kia. Hãy thảo luận để làm rõ nhận xét này. Phương pháp giải: Dựa vào lý thuyết về khoảng cách đã học của bài Lời giải chi tiết: - Khoảng cách từ một điểm M đến một đường thẳng a là khoảng cách giữa M và hình chiếu H của M trên a. - Khoảng cách từ điểm M đến mặt phẳng (P) là khoảng cách giữa M và hình chiếu H của M trên (P) - Khoảng cách giữa đường thẳng a và mặt phẳng (P) song song với a là khoảng cách từ một điểm bất kì trên a đến (P). - Khoảng cách giữa hai mặt phẳng song song (P) và (Q) là khoảng cách từ một điểm bất kì thuộc mặt phẳng này đến mặt phẳng kia. Mà đường vuông góc là đường ngắn nhất nên khoảng cách giữa hai hình được nêu trong bài học (điểm, đường thẳng, mặt phẳng) là khoảng cách nhỏ nhất giữa một điểm thuộc hình này và một điểm thuộc hình kia.
>> 2K8 Chú ý! Lộ Trình Sun 2026 - 3IN1 - 1 lộ trình ôn 3 kì thi (Luyện thi 26+TN THPT, 90+ ĐGNL HN, 900+ ĐGNL HCM; 70+ ĐGTD - Click xem ngay) tại Tuyensinh247.com.Đầy đủ theo 3 đầu sách, Thầy Cô giáo giỏi, 3 bước chi tiết: Nền tảng lớp 12; Luyện thi chuyên sâu; Luyện đề đủ dạng đáp ứng mọi kì thi.
|