Giải mục 1 trang 52, 53 SGK Toán 8 tập 2– Chân trời sáng tạo

HĐ1

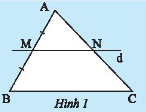
Cho tam giác $ABC$, vẽ đường thẳng $d$ đi qua trung điểm $M$ của cạnh $AB$, song song với cạnh $BC$ và cắt $AC$ tại $N$ (Hình 1). Hãy chứng minh $N$ là trung điểm của $AC$.

Phương pháp giải:

Sử dụng định lí Thales

Nếu một đường thẳng song song với một cạnh của tam giác và cắt hai cạnh còn lại thì nó định ra trên hai cạnh đó các đoạn thẳng tương ứng tỉ lệ.

Lời giải chi tiết:

Xét tam giác $ABC$ có $MN//BC$ nên áp dụng định lí Thales cho tam giác ta có:

$\frac{{AM}}{{AB}} = \frac{{AN}}{{AC}}$.

Mà $M$ là trung điểm của $AB$ nên $AM = \frac{1}{2}BC$ hay $\frac{{AM}}{{BC}} = \frac{1}{2}$.

Do đó, $\frac{{AM}}{{AB}} = \frac{{AN}}{{AC}} = \frac{1}{2}$ suy ra $\frac{{AN}}{{AC}} = \frac{1}{2}$ nên $AN = \frac{1}{2}AC$.

Do đó, $N$ là trung điểm của $AC$.

TH1

Tìm độ dài đoạn thẳng $NQ$ trong Hình 4.

Phương pháp giải:

Sử dụng định lí Thales

Nếu một đường thẳng song song với một cạnh của tam giác và cắt hai cạnh còn lại thì nó định ra trên hai cạnh đó các đoạn thẳng tương ứng tỉ lệ.

Lời giải chi tiết:

Từ hình vẽ ta có: $\widehat {OMN} = \widehat {OPQ}$.

Mà hai góc này ở vị trí đồng vị nên $MN//PQ$

Xét tam giác $OPQ$ có $MN//PQ$ nên áp dụng định lí Thales cho tam giác ta có:

$\frac{{OM}}{{MP}} = \frac{{ON}}{{NQ}}$

$\frac{5}{5} = \frac{4}{{NQ}}$

suy ra $NQ = \frac{{4.5}}{5} = 4$.

Vậy $NQ = 4$.

VD1

Trong Hình 5, chứng minh $MN$ là đường trung bình của tam giác $ABC$.

Phương pháp giải:

- Đường trung bình của tam giác là đoạn thẳng nối hai trung điểm hai cạnh tam giác.

- Hệ quả của định lí Thales

Nếu một đường thẳng cắt hai cạnh của một tam giác và song song với cạnh thứ ba thì tạo ra một tam giác mới có ba cạnh tương ứng tỉ lệ với ba cạnh của tam giác đã cho.

Lời giải chi tiết:

Vì $\left\{ \begin{array}{l}MN \bot AB\\CA \bot AB\end{array} \right.$ nên $MN//CA$ (Quan hệ từ vuông góc đến song song).

Ta có:

$AM = BM$ và $BM = \frac{1}{2}AB$ nên $\frac{{BM}}{{AB}} = \frac{1}{2}$ hay $M$ là trung điểm của $AB$.

Xét tam giác $ABC$ có $NM//AC;MN$ cắt $BA;BC$ lần lượt tại $M;N$. Theo hệ quả của định lí Thales ta có:

$\frac{{BM}}{{AB}} = \frac{{BN}}{{BC}}$

$\frac{{BN}}{{BC}} = \frac{1}{2}$

Hay $2BN = BC$. Do đó, $N$ là trung điểm của $BC$.

Xét tam giác $ABC$ có:

$M$ là trrung điểm của $AB$

$N$ là trrung điểm của $BC$

Do đó, $MN$ là đường trung bình của tam giác $ABC$ (điều phải chứng minh).