Giải mục 1 trang 50, 51 Chuyên đề học tập Toán 10 - Chân trời sáng tạoCho hypebol (H) với phương trình chính tắc x2a2−y2b2=1 và điểm M(x0;y0) nằm trên (H). Các điểm M1(−x0;y0),M2(x0;−y0),M3(−x0;−y0) có thuộc (H) không? Tổng hợp đề thi học kì 2 lớp 10 tất cả các môn - Chân trời sáng tạo Toán - Văn - Anh - Lí - Hóa - Sinh - Sử - Địa...
Lựa chọn câu để xem lời giải nhanh hơn
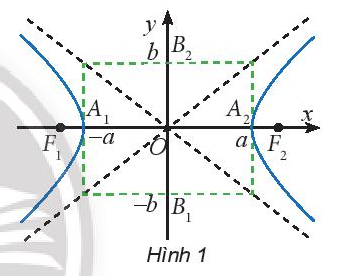
HĐ1 Cho hypebol (H) với phương trình chính tắc x2a2−y2b2=1 và điểm M(x0;y0) nằm trên (H). Các điểm M1(−x0;y0),M2(x0;−y0),M3(−x0;−y0) có thuộc (H) không?
Lời giải chi tiết: Nếu điểm M(x0;y0) thuộc hypebol thì x02a2−y02b2=1 ⇒(−x0)2a2−y02b2=1;x02a2−(−y0)2b2=1;(−x0)2a2−(−y0)2b2=1 hay các điểm M1(−x0;y0),M2(x0;−y0),M3(−x0;−y0)cũng thuộc Hypebol. Thực hành 1 Viết phương trình chính tắc của Hypebol có kích thước của hình chữ nhật cơ sở là 8 và 6. Hãy xác định đỉnh, tiêu điểm, tiêu cự, độ dài trục của Hypebol này. Phương pháp giải: Phương trình của hypebol x2a2−y2b2=1 Trong đó: + 4 đỉnh là A1(−a;0),A2(a;0),B1(0;−b),B2(0;b). + Kích thước của hình chữ nhật cơ sở là 2a và 2b. + Tiêu điểm F1(−c;0),F2(c;0), + Tiêu cự: 2c=2√a2+b2 + Độ dài trục thực: 2a, độ dài trục ảo: 2b Lời giải chi tiết: + Kích thước của hình chữ nhật cơ sở là 2a=8 và 2b=6. ⇒a=4,b=3,c=√a2+b2=5 + 4 đỉnh là A1(−4;0),A2(4;0),B1(0;−3),B2(0;3). + Tiêu điểm F1(−5;0),F2(5;0), + Tiêu cự: 2c=10 + Độ dài trục thực: 2a=8, độ dài trục ảo: 2b=6.
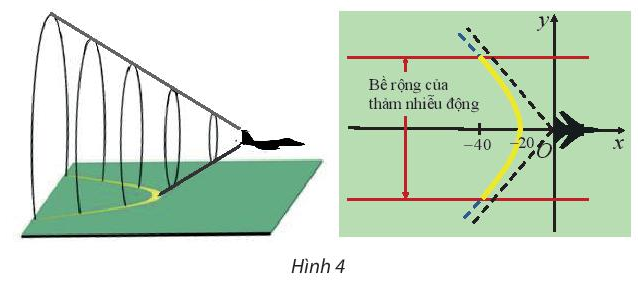
Vận dụng 1 Khi bay với vận tốc siêu thanh (tốc độ chuyển động lớn hơn tốc độ âm thanh trong cùng môi trường), một máy bay tạo ra một vùng nhiễu động trên mặt đất dọc theo một nhánh của hypebol (H) (Hình 4). Phần nghe rõ nhất tiếng ồn của vùng nói trên được gọi là thảm nhiễu động. Bề rộng của thảm này gấp khoảng 5 lần cao độ của máy bay. Tính cao độ của máy bay, biết bề rộng của thảm nhiễu động được đo cách phía sau máy bay một khoảng là 40mile (mile (dặm) là đơn vị đo khoảng cách, 1 mile ≈ 1,6 km) và (H) có phương trình: x2400−y2100=1
Lời giải chi tiết: + Bề rộng của thảm nhiễu động là 2|yM|, với M∈(H) và xM=−40 + Cao độ của máy bay: h=2|yM|5 Lời giải chi tiết + Bề rộng của thảm nhiễu động là 2|yM|, với M∈(H) và xM=−40 ⇔(−40)2400−yM2100=1⇔yM=±10√3 + Cao độ của máy bay: h=2|yM|5=2.10√35=4√3 (mile) ≈4√3.1,6≈11 (km).
>> Học trực tuyến Lớp 10 cùng thầy cô giáo giỏi tại Tuyensinh247.com, (Xem ngay) Cam kết giúp học sinh học tốt, bứt phá điểm 9,10 chỉ sau 3 tháng, làm quen kiến thức, định hướng luyện thi TN THPT, ĐGNL, ĐGTD ngay từ lớp 10
|