Giải mục 1 trang 41, 42, 43 SGK Toán 7 tập 1 - Kết nối tri thứcQuan sát hình vẽ bên. Em hãy nhận xét về mối quan hệ về đỉnh, về cạnh của hai góc được đánh dấu...Cho ba tia Ox, Oy, Oz như Hình 3.1, trong đó Ox và Oy là hai tia đối nhau. a) Em hãy nhận xét về quan hệ về đỉnh, về cạnh của hai góc xOz và zOy. b) Đo rồi tính tổng số đo góc hai góc xOz và zOy. Tổng hợp đề thi học kì 2 lớp 7 tất cả các môn - Kết nối tri thức Toán - Văn - Anh - Khoa học tự nhiên...
Lựa chọn câu để xem lời giải nhanh hơn
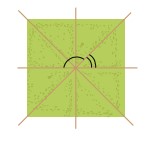
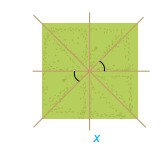
HĐ 1 Quan sát hình vẽ bên. Em hãy nhận xét về mối quan hệ về đỉnh, về cạnh của hai góc được đánh dấu.
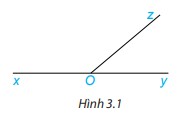
Phương pháp giải: Xác định đỉnh, cạnh của hai góc được đánh dấu rồi nhận xét. Lời giải chi tiết: 2 góc được đánh dấu là 2 góc có: chung đỉnh; có chung một cạnh, cạnh còn lại là 2 tia đối nhau HĐ 2 Cho ba tia Ox, Oy, Oz như Hình 3.1, trong đó Ox và Oy là hai tia đối nhau. a) Em hãy nhận xét về quan hệ về đỉnh, về cạnh của hai góc xOz và zOy. b) Đo rồi tính tổng số đo góc hai góc xOz và zOy.
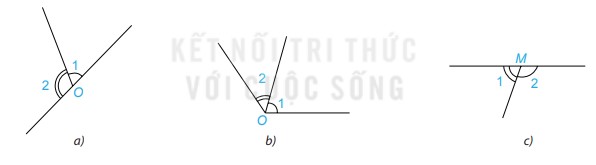
Phương pháp giải: a) Xác định đỉnh, cạnh của hai góc được đánh dấu rồi nhận xét. b) Đo góc: đặt đỉnh của góc trùng với gốc của thước, 1 cạnh của góc trùng với vạch 0, cạnh còn lại của góc trùng với vạch nào thì đó là số đo góc. Lời giải chi tiết: a) Đỉnh của góc xOz và zOy cùng là đỉnh O 2 góc xOz và zOy có chung cạnh Oz, cạnh còn lại (Ox và Oy) là 2 tia đối nhau. b) \(\widehat{xOz}=140^0, \widehat{zOy}=40^0\) Ta được: \(\widehat{xOz}+\widehat{zOy}=140^0+40^0=180^0\) Câu hỏi 1 Hai góc được đánh dấu trong hình nào dưới đây là hai góc kề bù?
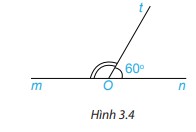
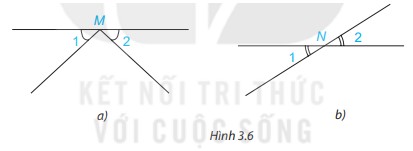
Phương pháp giải: 2 góc có một cạnh chung, hai cạnh còn lại là hai tia đối nhau được gọi là 2 góc kề bù Lời giải chi tiết: Xét hình a: \(\widehat {{O_1}}\) và \( \widehat {{O_2}}\) là hai góc kề bù vì 2 góc này có một cạnh chung, hai cạnh còn lại là hai tia đối nhau Xét hình b: \(\widehat {{O_1}} \) và \( \widehat {{O_2}}\) không là hai góc kề bù vì 2 góc này có một cạnh chung nhưng hai cạnh còn lại không là hai tia đối nhau Xét hình c: \(\widehat {{M_1}} \) và \( \widehat {{M_2}}\) là hai góc kề bù vì 2 góc này có một cạnh chung, hai cạnh còn lại là hai tia đối nhau. Luyện tập 1 Viết tên hai góc kề bù trong Hình 3.4 và tính số đo góc mOt
Phương pháp giải: 2 góc có một cạnh chung, hai cạnh còn lại là hai tia đối nhau được gọi là 2 góc kề bù. Tổng số đo của 2 góc kề bù là 180 độ. Lời giải chi tiết: 2 góc kề bù trong hình là: góc mOt và tOn Ta có: \(\begin{array}{l}\widehat {mOt} + \widehat {tOn} = 180^\circ \\\widehat {mOt} = 180^\circ - \widehat {tOn} = 180^\circ - 60^\circ = 120^\circ \end{array}\) HĐ 3 Quan sát hình ảnh hai góc được đánh dấu trong hình bên. Em hãy nhận xét quan hệ về đỉnh, về cạnh của hia góc được đánh dấu.
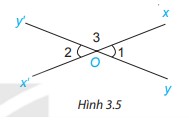
Phương pháp giải: Xác định đỉnh, cạnh của hai góc được đánh dấu rồi nhận xét. Lời giải chi tiết: 2 góc trên hình có cùng đỉnh; từng cạnh của góc này là tia đối của cạnh của góc kia. HĐ 4 Cho hai đường thẳng xx’ và yy’ cắt nhau tại O (H.3.5) a) Dự đoán xem hai góc xOy và x’Oy’ có bằng nhau không? b) Đo rồi so sánh số đo hai góc xOy và x’Oy’
Phương pháp giải: Đo 2 góc rồi so sánh Lời giải chi tiết: a) Em dự đoán xem hai góc xOy và x’Oy’ có bằng nhau. b) \(\widehat{xOy} = \widehat{x’Oy’} = 31^0\) Câu hỏi 2 Hai góc được đánh dấu trong hình nào dưới đây là hai góc đối đỉnh?
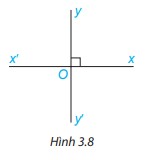
Phương pháp giải: Hai góc đối đỉnh là hai góc mà mỗi cạnh của góc này là tia đối của một cạnh của góc kia. Lời giải chi tiết: 2 góc ở hình 3.6.b là hai góc đối đỉnh vì 2 góc này có mỗi cạnh của góc này là tia đối của một cạnh của góc kia. Luyện tập 2 Hai đường thẳng xx’ và yy’ cắt nhau tại O sao cho góc xOy vuông (H.3.8). Khi đó các góc yOx’, x’Oy’, xOy’ cũng đều là góc vuông. Vì sao?
Phương pháp giải: Sử dụng tính chất: 2 góc kề bù có tổng là 180 độ, 2 góc đối đỉnh bằng nhau. Lời giải chi tiết: Góc x’Oy’ và xOy là hai góc đối đỉnh nên \(\widehat {x'Oy'} = \widehat {xOy} = 90^\circ \) Góc xOy’ và xOy là hai góc kề bù nên \(\begin{array}{l}\widehat {xOy'} + \widehat {xOy} = 180^\circ \\ \Rightarrow \widehat {xOy'} + 90^\circ = 180^\circ \\ \Rightarrow \widehat {xOy'} = 180^\circ - 90^\circ = 90^\circ \end{array}\) Góc x’Oy và xOy là hai góc kề bù nên \(\begin{array}{l}\widehat {x'Oy} + \widehat {xOy} = 180^\circ \\ \Rightarrow \widehat {x'Oy} + 90^\circ = 180^\circ \\ \Rightarrow \widehat {x'Oy} = 180^\circ - 90^\circ = 90^\circ \end{array}\)
|