Giải mục 1 trang 38, 39, 40 SGK Toán 10 tập 2 - Chân trời sáng tạo

HĐ Khởi động

Lời giải chi tiết:

Bàn cờ được chia thành 8 hàng (1-8) và 8 cột (a-h) đánh số như hình vẽ.

Do đó mỗi quân cờ xác định khi biết số hàng và số cột, tương ứng với cặp số (x;y) trong đó x là số hàng, y là số cột.

Khi đó hai mã đen có vị trí là (8;b) và (4;e)

Hai mã trắng có vị trí là (3;c) và (3;f)

Cách 2:

Đặt gốc tọa độ tại góc dưới, bên trái của bàn cờ. Coi mỗi ô vuông là 1 đơn vị.

Ta xác định được tọa độ của các con mã như sau:

Hai mã đen có tọa độ lần lượt là (2;8), (5;4)

Hai mã trắng có tọa độ lần lượt là (3;3) và (6;3)

HĐ Khám phá 1

Nêu nhận xét về độ lớn, phương và chiều của vectơ  trên trục $Ox$ và vectơ $\overrightarrow j$ trên trục $Oy$ (hình 1)

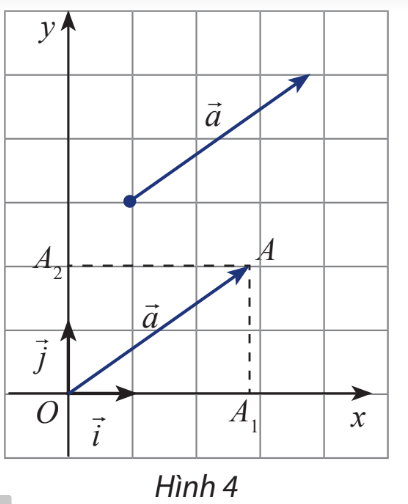
Lời giải chi tiết:

+) Vectơ  có độ lớn bằng 1 đơn vị, phương song song với trục $Ox$và cùng chiều với $Ox$

+) Vectơ $\overrightarrow j$ có độ lớn bằng 1 đơn vị, phương song song với trục $Oy$và cùng chiều với $Oy$

HĐ Khám phá 2

Trong mặt phẳng Oxy, cho một vectơ $\overrightarrow a$tùy ý. Vẽ $\overrightarrow {OA}  = \overrightarrow a$và gọi ${A_1},{A_2}$lần lượt là hình chiếu vuông góc của A lên Ox và  Oy (hình 4). Đặt ${\overrightarrow {OA} _1} = x\overrightarrow i$, ${\overrightarrow {OA} _2} = y\overrightarrow j$. Biểu diễn vectơ $\overrightarrow a$theo hai vectơ  và $\overrightarrow j$

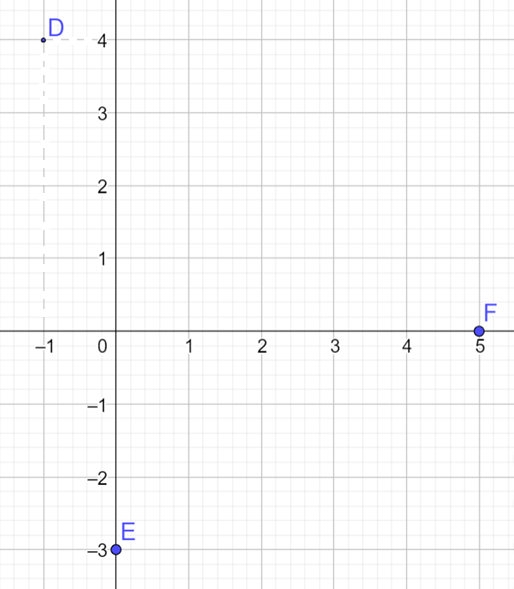
Phương pháp giải:

Bước 1: Áp dụng quy tắc hình bình hành $\overrightarrow {AC}  = \overrightarrow {AB}  + \overrightarrow {AD}$

Bước 2: Dựa vào hình vẽ tìm x,y

Bước 3: Biểu diễn vectơ $\overrightarrow a$

Lời giải chi tiết:

Áp dụng quy tắc hình bình hành ta có $\overrightarrow {OA}  = \overrightarrow {O{A_1}}  + \overrightarrow {O{A_2}}$

Dựa vào hình vẽ ta thấy ${\overrightarrow {OA} _1} = 3\overrightarrow i$ và ${\overrightarrow {OA} _2} = 2\overrightarrow j$

Vậy $\overrightarrow a  = \overrightarrow {OA}  = \overrightarrow {O{A_1}}  + \overrightarrow {O{A_2}}  = 3\overrightarrow i  + 2\overrightarrow j$

HĐ Khám phá 3

Trong mặt phẳng Oxy, cho điểm M. Xác định tọa độ của vectơ $\overrightarrow {OM}$

Phương pháp giải:

Bước 1: Từ điểm M(x;y) xác định ${M_1},{M_2}$ lần lượt là hình chiếu vuông  góc của M xuống trục hoành và trục tung

Bước 2: Tìm m, n sao cho $\overrightarrow {OM_1}= m.\overrightarrow {i}; \, \overrightarrow {OM_2}=n.\overrightarrow {j}$

Bước 3: Dựa vào quy tắc hình bình hành, suy ra tọa độ của vectơ $\overrightarrow {OM}$ theo $\overrightarrow {i}; \overrightarrow {j}$.

Lời giải chi tiết:

Cho điểm M(x;y) bất kì, xác định ${M_1},{M_2}$ lần lượt là hình chiếu vuông  góc của M xuống trục hoành và trục tung

Dễ thấy $\overrightarrow {O{M_1}}= x\overrightarrow i ; \, \overrightarrow {O{M_2}}  = y \overrightarrow j$

Áp dụng quy tắc hình bình hành ta có $\overrightarrow {OM}  = \overrightarrow {O{M_1}}  + \overrightarrow {O{M_2}}  = x\overrightarrow i  + y\overrightarrow j$

Vậy tọa độ của vectơ $\overrightarrow {OM}$ là (x;y), trùng với tọa độ điểm M.

Thực hành 1

Trong mặt phẳng Oxy, cho ba điểm $D\left( { - 1;4} \right),E\left( {0; - 3} \right),F\left( {5;0} \right)$

a) Vẽ các điểm D, E, F trên mặt phẳng Oxy

b) Tìm tọa độ của các vectơ $\overrightarrow {OD} ,\overrightarrow {OE} ,\overrightarrow {OF}$.

c) Vẽ và tìm tọa độ hai vectơ đơn vị  và $\overrightarrow j$lần lượt trên hai trục tọa độ Ox và Oy

Lời giải chi tiết:

a) 

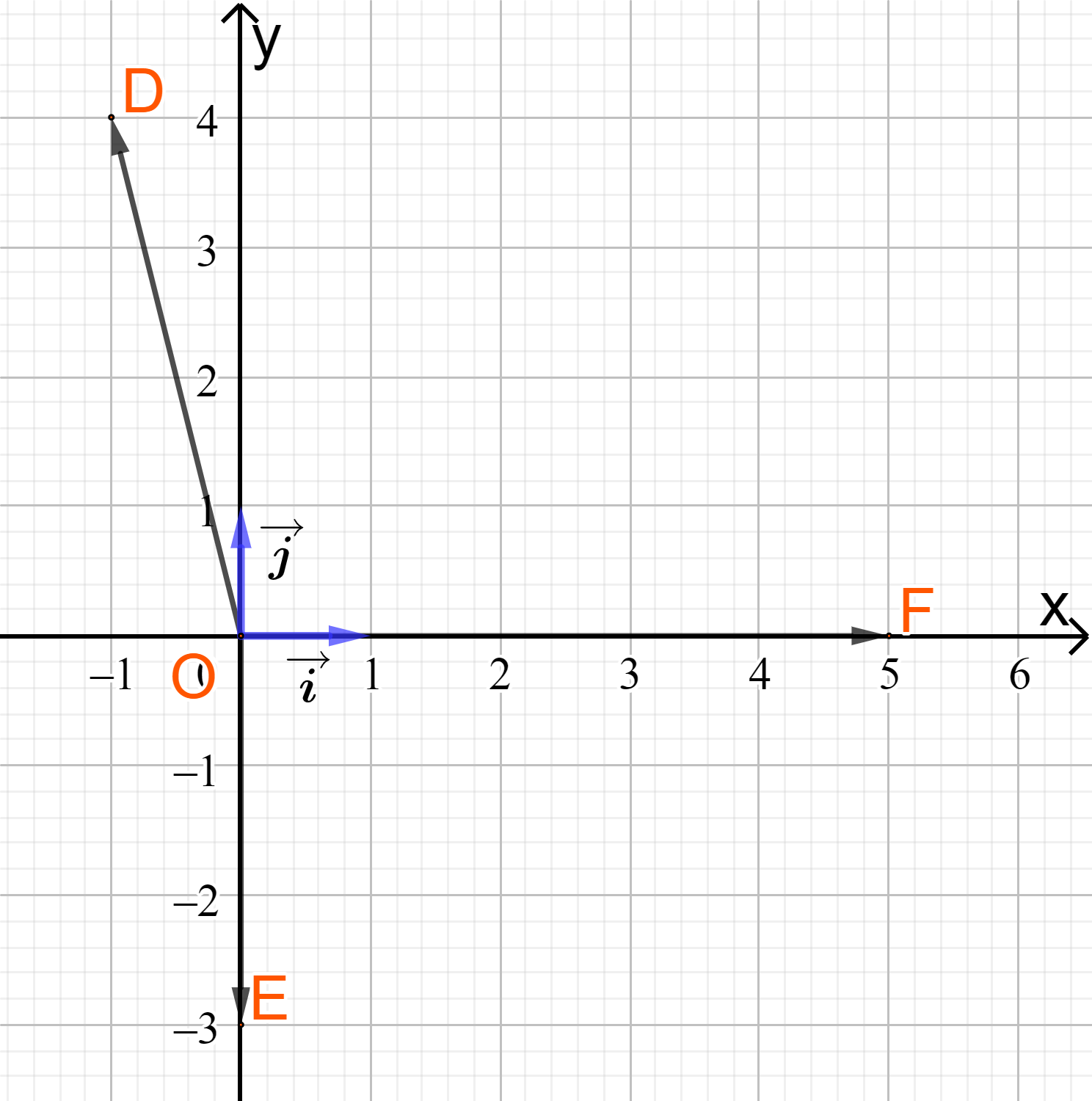
b) Vì tọa độ vectơ $\overrightarrow {OM}$ chính là tọa độ của điểm M (với mọi M) nên ta có:

$\overrightarrow {OD}  = \left( { - 1;4} \right),\overrightarrow {OE}  = \left( {0; - 3} \right),\overrightarrow {OF}  = \left( {5;0} \right)$

c) 

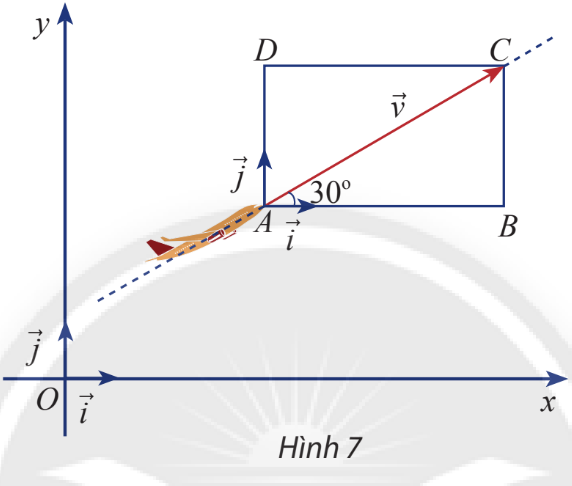
Từ hình vẽ ta có tọa độ của hai vectơ   và $\overrightarrow j$là

 và $\overrightarrow j  = (0;1)$

Vận dụng 1

Một máy bay đang cất cánh với vận tốc 240 km/h theo phương hợp với phương nằm ngang một góc $30^\circ$ (hình 7)

a) Tính độ dài mỗi cạnh của hình chữ nhật ABCD

b) Biểu diễn vận tốc $\overrightarrow v$ theo hai vectơ  và $\overrightarrow j$

c) Tìm tọa độ của $\overrightarrow v$

Lời giải chi tiết:

a) Vận tốc 240 km/h nên $\left| {\overrightarrow v } \right| = AC = 240$

Áp dụng các tính chất trong tam giác vuông ta có

$AB = DC = AC.\cos (\widehat {CAB}) = 240.\cos (30^\circ ) = 120{\sqrt 3 }$

$AD = BC = AC.\sin (\widehat {CAB}) = 240.\sin (30^\circ ) = 120$

b) Xem A là gốc tọa độ nên ta có $\overrightarrow {AB}  = 120\overrightarrow i ,\overrightarrow {AD}  = 120{\sqrt 3 }\overrightarrow j ,\overrightarrow v  = \overrightarrow {AC}  = 120\overrightarrow i  + 120{\sqrt 3 }\overrightarrow j$

c)

Ta có $\overrightarrow v  = 120\overrightarrow i  + 120{\sqrt 3 }\overrightarrow j$

Vậy tọa độ của vectơ $\overrightarrow v$ là $\left( {120;120{\sqrt 3 }} \right)$