C. Hoạt động ứng dụng - Bài 56 : Diện tích hình tam giácGiải bài 56 : Diện tích hình tam giác phần hoạt động ứng dụng trang 148 sách VNEN toán lớp 5 với lời giải dễ hiểu
Lựa chọn câu để xem lời giải nhanh hơn
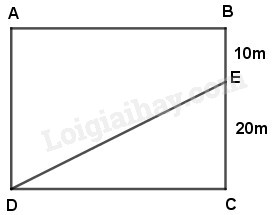
Câu 1 Cho biết diện tích của thửa ruộng hình chữ nhật ABCD là \(1200{m^2}\) (xem hình vẽ). Tính diện tích của mảnh ruộng hình tam giác DCE.
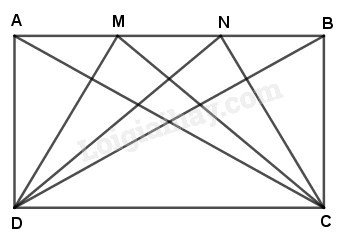
Phương pháp giải: - Tìm chiều dài của hình chữ nhật ( chính bằng cạnh đáy của hình tam giác DCE). - Diện tích tam giác DCE bằng độ dài cạnh đáy vừa tìm được nhân với chiều cao tương ứng. Lời giải chi tiết: Chiều dài của mảnh ruộng hình chữ nhật ABCD là: \( 1200 : (20 + 10) = 40 \;(m)\) Ta có: Tam giác DCE có đường cao EC = 20m và cạnh đáy CD = 40m. Vậy diện tích của mảnh ruộng hình tam giác DCE là: \(\left( {40 \times 20} \right):2 = {\rm{ }}400\;{\rm{ }}({m^2})\) Đáp số: \(400{m^2}\). Câu 2 a) Quan sát các hình vẽ dưới đây, biết \(AM = MN = NB\), em hãy nhận xét về diện tích các hình tam giác \(ADC, MDC, NCD\) và \(BDC\).
b) Em hãy chỉ ra các hình tam giác có diện tích bằng nhau ở trong hình vẽ trên. Phương pháp giải: - Dựa vào kiến thức về diện tích hình tam giác vừa học, nhận xét về diện tích các hình. - Quan sát hình ảnh và đọc dữ kiện trong bài toán, tìm các tam giác có độ dài đáy và chiều cao tương ứng bằng nhau. Lời giải chi tiết: a) Tam giác ADC, MDC, NDC, BDC có : - Cạnh đáy DC chung. - Chiều cao tương ứng kẻ từ các đỉnh A, M, N, B tới cạnh đáy BC đều bằng nhau. Vậy diện tích các hình tam giác ADC, MDC, NDC, BDC bằng nhau. b) Các hình tam giác có diện tích bằng nhau trong hình đã cho là : - Các tam giác ADC, MDC, NDC, BDC có diện tích bằng nhau (câu a). - Các tam giác DAB và CAB có diện tích bằng nhau (cùng chung cạnh đáy AB, chiều cao AD = BC). - Các tam giác DAM, DMN, DNB, CAM, CMN, CNB có diện tích bằng nhau (có cạnh đáy AM = MN = NB và chiều cao \(AD = BC\)). - Các tam giác AND, MDB, CBM, CNA có diện tích bằng nhau (cạnh đáy AN = MB = BM = AN và chiều cao tương ứng \(AD = BC\)). HocTot.Nam.Name.Vn
|