A. Hoạt động thực hành - Bài 8 : Em ôn lại những gì đã họcGiải Bài 8 : Em ôn lại những gì đã học phần hoạt động thực hành trang 22, 23 sách VNEN toán lớp 5 với lời giải dễ hiểu
Lựa chọn câu để xem lời giải nhanh hơn
Câu 1 Tính :
Phương pháp giải: a) - Muốn cộng (hoặc trừ) hai phân số khác mẫu số ta quy đồng mẫu số rồi cộng (hoặc trừ) các phân số sau khi quy đồng. - Muốn nhân hai phân số ta lấy tử số nhân với tử số, mẫu số nhân với mẫu số. - Muốn chia hai phân số ta lấy phân số thứ nhất nhân với phân số thứ hai đảo ngược. b) - Đổi các hỗn số thành phân số, sau đó thực hiện các phép tính cộng, trừ, nhân, chia hai phân số như thông thường. - Biểu thức chỉ có phép cộng và phép trừ ta thực hiện lần lượt từ trái sang phải. Lời giải chi tiết: a) \(\dfrac{7}{8} - \dfrac{1}{3} = \dfrac{{21}}{{24}} - \dfrac{8}{{24}} = \dfrac{{13}}{{24}}\); \(\dfrac{8}{9} + \dfrac{2}{5} = \dfrac{{40}}{{45}} + \dfrac{{18}}{{45}} = \dfrac{{58}}{{45}}\); \(\dfrac{3}{{10}} \times \dfrac{1}{6} = \dfrac{{3 \times 1}}{{10 \times 6}} = \dfrac{3}{{60}} = \dfrac{1}{{20}}\); \(\dfrac{8}{9}:\dfrac{3}{7} = \dfrac{8}{9} \times \dfrac{7}{3} = \dfrac{{56}}{{27}}\). b) \(1\dfrac{2}{7} + 6\dfrac{5}{6} = \dfrac{9}{7} + \dfrac{{41}}{6} = \dfrac{{54}}{{42}} + \dfrac{{287}}{{42}} \)\( = \dfrac{{341}}{{42}}\); \(5\dfrac{3}{4} - \dfrac{1}{5} = \dfrac{{23}}{4} - \dfrac{1}{5} = \dfrac{{115}}{{20}} - \dfrac{4}{{20}} \)\(= \dfrac{{111}}{{20}}\) ; \(6\dfrac{2}{9}:4\dfrac{7}{{10}} = \dfrac{{56}}{9}:\dfrac{{47}}{{10}} = \dfrac{{56}}{9} \times \dfrac{{10}}{{47}} \)\(= \dfrac{{560}}{{423}}\) ; \(\dfrac{5}{3} + \dfrac{3}{2} - \dfrac{7}{6} = \dfrac{{10}}{6} + \dfrac{9}{6} - \dfrac{7}{6} \)\(= \dfrac{{19}}{6} - \dfrac{7}{6} = \dfrac{{12}}{6} = 2\) Câu 2 Tìm \(x\) : a) \(x + \dfrac{2}{3} = \dfrac{9}{{11}}\) ; b) \(x - \dfrac{3}{{10}} = \dfrac{4}{{15}}\); c) \(x \times \dfrac{1}{7} = \dfrac{5}{6}\) ; d) \(x:\dfrac{3}{5} = \dfrac{1}{6}\) Phương pháp giải: Xác định vai trò của \(x\) trong phép tính rồi thực hiện theo các quy tắc đã học: - Muốn tìm số hạng chưa biết ta lấy tổng trừ đi số hạng đã biết. - Muốn tìm số bị trừ ta lấy hiệu cộng với số trừ. - Muốn tìm thừa số chưa biết ta lấy tích chia cho thừa số đã biết. - Muốn tìm số bị chia ta lấy thương nhân với số chia. Lời giải chi tiết: \(\begin{array}{l}a) \;x + \dfrac{2}{3} = \dfrac{9}{{11}}\\ \quad x = \dfrac{9}{{11}} - \dfrac{2}{3}\\\quad x = \dfrac{5}{{33}}\end{array}\) \(\begin{array}{l}b)\;x - \dfrac{3}{{10}} = \dfrac{4}{{15}}\\ \quad x = \dfrac{4}{{15}} + \dfrac{3}{{10}}\\ \quad x = \dfrac{{17}}{{30}}\end{array}\) \(\begin{array}{l}c)\;x \times \dfrac{1}{7} = \dfrac{5}{6}\\ \quad x = \dfrac{5}{6}:\dfrac{1}{7}\\ \quad x = \dfrac{{35}}{6}\end{array}\) \(\begin{array}{l}d)\; x:\dfrac{3}{5} = \dfrac{1}{6}\\ \quad x = \dfrac{1}{6} \times \dfrac{3}{5}\\ \quad x = \dfrac{1}{{10}}\end{array}\) Câu 3 Viết (theo mẫu) : a)
\(23m{\rm{ }}18cm{\rm{ }}\;;\;\;\;\;\;\; 9m{\rm{ }}5cm.\) b)
\(7kg{\rm{ }}\;167g{\rm{ }}\;;\;\;\; \;34kg{\rm{ }}\;50g{\rm{ }}\;;\;\;\; 1kg{\rm{ }}5g\) Phương pháp giải: - Áp dụng cách chuyển đổi : \(1m = 100cm\,\,;\,\,\,1cm = \dfrac{1}{{100}}m\,\, ;\) \(1kg = 1000g\,;\,\,\,1g = \dfrac{1}{{1000}}kg.\) - Quan sát các ví dụ mẫu và làm tương tự như thế. Lời giải chi tiết: a) \(23m\,\,18cm = 23m + \dfrac{{18}}{{100}}m \)\(= 23\dfrac{{18}}{{100}}m;\) \(9m\,\,5cm = 9m + \dfrac{5}{{100}}m = 9\dfrac{5}{{100}}m.\) b) \(7kg\,\,167g = 7kg + \dfrac{{167}}{{1000}}kg \)\(= 7\dfrac{{167}}{{1000}}kg.\) \(34kg\,\,50g = 34kg + \dfrac{{50}}{{1000}}kg \)\(= 34\dfrac{{50}}{{1000}}kg.\) \(1kg\,\,5g = 1kg + \dfrac{5}{{1000}}kg\)\(= 1\dfrac{5}{{1000}}kg.\) Câu 4 Biết \(\dfrac{2}{5}\) quãng đường AB dài \(36km\). Hỏi quãng đường AB dài bao nhiêu ki-lô-mét ?
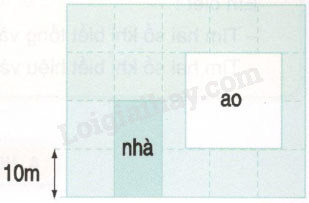
Phương pháp giải: - Tìm độ dài của \(\dfrac{1}{5}\) quãng đường ta lấy \(36km\) chia cho \(2\) . - Tìm độ dài quãng đường ta lấy độ dài của \(\dfrac{1}{5}\) quãng đường nhân với \(5\). Lời giải chi tiết: \(\dfrac{1}{5}\) quãng đường AB dài số ki-lô-mét là : \(36:2 = 18\,\,(km)\) Quãng đường AB dài số ki-lô-mét là : \(18 \times 5 = 90\,\,(km)\) Đáp số : \(90km.\) Câu 5 Một mảnh đất hình chữ nhật có kích thước như hình vẽ bên (h12) :
Sau khi đào ao và làm nhà thì diện tích phần đất còn lại là : \(A.\; 180{m^2}\) \(B. \;1400{m^2}\) \(C. \;1800{m^2}\) \(D. \;2000{m^2}\) Phương pháp giải: - Diện tích mảnh đất bằng diện tích hình chữ nhật có chiều dài 50m (bằng 5 ô vuông) và chiều rộng 40m (bằng 4 ô vuông). Để tính diện tích mảnh đất ta lấy chiều dài nhân với chiều rộng. - Diện tích làm nhà bằng diện tích hình chữ nhật có chiều dài 20m (bằng 2 ô vuông) và chiều rộng 10m (bằng 1 ô vuông). Để tính diện tích làm nhà ta lấy chiều dài nhân với chiều rộng. - Diện tích làm ao bằng diện tích hình vuông có độ dài cạnh là 20m (bằng 2 ô vuông). Để tính diện tích đào ao ta lấy cạnh nhân với cạnh. - Diện tích phần đất còn lại = diện tích mảnh đất - (diện tích đào ao + diện tích làm nhà). Lời giải chi tiết: Chiều dài mảnh đất là: 10 × 5 = 50 (m) Chiều rộng mảnh đất là: 10 × 4 = 40 (m) Diện tích mảnh đất là: 50 × 40 = 2000 (\(m^2\)) Chiều dài nhà là: 10 × 2 = 20 (m) Chiều rộng nhà là: 10 × 1 = 10 (m) Diện tích nhà là: 20 × 10 = 200 (\(m^2\)) Ao hình vuông có cạnh dài là: 10 × 2 = 20 (m) Diện tích ao là: 20 × 20 = 400 (\(m^2\)) Diện tích phần đất còn lại là: 2000 - (400 + 200) = 1400 (\(m^2\)) Khoanh vào B. HocTot.Nam.Name.Vn
|