B. Hoạt động thực hành - Bài 59 : Diện tích hình thangGiải Bài 59 : Diện tích hình thang phần hoạt động thực hành trang 8 sách VNEN toán lớp 5 với lời giải dễ hiểu
Lựa chọn câu để xem lời giải nhanh hơn
Câu 1 Tính diện tích hình thang, biết : a) Độ dài hai đáy lần lượt là 14cm và 11cm; chiều cao là 4cm. b) Độ dài hai đáy lần lượt là 8,7m và 6,3m; chiều cao là 5,7m. Phương pháp giải: Áp dụng cách tính diện tích hình thang : Diện tích hình thang bằng tổng độ dài hai đáy nhân với chiều cao (cùng một đơn vị đo) rồi chia cho 2. Lời giải chi tiết: a) Diện tích hình thang đó là : \( \dfrac{(14+11) \times 4}{2} = 50\;(cm^2)\) b) Diện tích hình thang đó là : \( \dfrac{(8,7+6,3 ) \times 5,7}{2} = 42,75\;(m^2)\) Câu 2 Tính diện tích hình thang có độ dài đáy lần lượt là a và b, chiều cao h : a) a =18cm ; b = 12cm ; h = 9cm. b) a = 34m ; b = 12m ; h = 58m. a) a =3,4dm ; b = 5,8dm ; h = 0,5dm. Phương pháp giải: Áp dụng công thức tính diện tích hình thang : \(S = \displaystyle {{\left( {a + b} \right) \times h} \over 2}\) trong đó \(S\) là diện tích; \(a,\,b\) là độ dài các cạnh đáy; \(h\) là chiều cao. Lời giải chi tiết: a) Diện tích hình thang là đó là : \( \dfrac{(18 + 12 ) \times 9}{2} = 135\;(cm^2)\) b) Diện tích hình thang là đó là : \(\dfrac{{\left( {\dfrac{3}{4} + \dfrac{1}{2}} \right) \times \dfrac{5}{8}}}{2} = \dfrac{{25}}{{64}}\,\,({m^2})\) c) Diện tích hình thang là đó là : \( \dfrac{( 3,4+ 5,8) \times 0,5}{2} = 2,3\;(dm^2)\) Câu 3 Giải bài toán sau : Một mảnh vườn hình thang có độ dài hai đáy lần lượt là 12m và 8,4m. Chiều cao bằng trung bình cộng của hai đáy. Tính diện tích mảnh vườn đó.
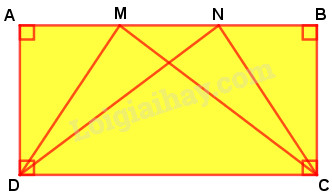
Phương pháp giải: - Tính chiều cao = (đáy lớn + đáy bé) : 2 - Diện tích mảnh vườn = (đáy lớn + đáy bé) × chiều cao : 2. Lời giải chi tiết: Chiều cao của mảnh vườn hình thang là : \((12 + 8,4) : 2= 10,2\; (m)\) Diện tích mảnh vườn hình thang là : \( \dfrac{( 12+ 8,4 ) \times 10,2}{2} = 104,04\;(m^2)\) Đáp số: \(104,04m^2.\) Câu 4 Đúng ghi Đ, sai ghi S ? a) Diện tích các hình thang AMCD, MNCD, NBCD bằng nhau. \(\square\) b) Diện tích hình thang AMCD bằng \(\dfrac{1}{3}\) diện tích hình chữ nhật ABCD. \(\square\)
Phương pháp giải: Áp dụng cách tính diện tích hình thang và diện tích hình chữ nhật : - Diện tích hình thang bằng tổng độ dài hai đáy nhân với chiều cao (cùng một đơn vị đo) rồi chia cho 2. - Diện tích hình chữ nhật bằng chiều dài nhân với chiều rộng. Lời giải chi tiết: a) Ba hình thang AMCD, MNCD, NBCD có diện tích bằng nhau vì chúng có chung đáy lớn DC, đáy bé bằng 2cm và có chiều cao bằng nhau là độ dài đoạn thẳng AD. Vậy ta ghi chữ Đ vào ô trống. b) Diện tích hình chữ nhật ABCD bằng: \(AB \times AD = 6 \times AD \). Diện tích hình thang AMCD bằng: \(\dfrac{{\left( {DC + AM} \right) \times AD}}{2} = \dfrac{{\left( {6 + 2} \right) \times AD}}{2}\)\( = 4 \times AD\) Ta có: \(\dfrac{{4 \times A{{D}}}}{{6 \times A{{D}}}} =\dfrac{4}{6}= \dfrac{2}{3}\) Do đó diện tích hình thang AMCD bằng \(\dfrac{2}{3}\) diện tích hình chữ nhật ABCD. Vậy ta ghi chữ S vào ô trống. HocTot.Nam.Name.Vn
|