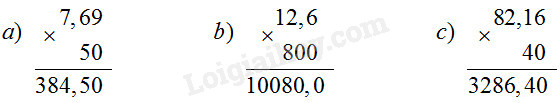B. Hoạt động thực hành - Bài 35 : Nhân một số thập phân với 10, 100, 1000, ...Giải Bài 35 : Nhân một số thập phân với 10, 100, 1000, ... phần hoạt động thực hành trang 95 sách VNEN toán lớp 5 với lời giải dễ hiểu
Lựa chọn câu để xem lời giải nhanh hơn
Câu 1 Đặt tính rồi tính : a) 7,69 × 50 b) 12,6 × 800 c) 82,16 × 40 Phương pháp giải: a) - Đặt tính. - Thực hiện phép nhân 7,69 với 5 rồi chuyển dấu phẩy của số đó lần lượt sang bên phải một chữ số. Thực hiện tương tự với các ý b;c. Lời giải chi tiết:
Câu 2 Viết các số đo sau dưới dạng số đo có đơn vị là mi-li-mét : a) 10,4dm b) 5,75cm c) 0,856m Phương pháp giải: - Nhớ lại kiến thức về bảng đơn vị đo độ dài : 1m = 1000mm; 1dm= 100mm; 1cm = 10mm. - Cách nhân một số thập phân với 10, 100, 1000 ... vừa học và thực hiện phép tính. Lời giải chi tiết: a) 10,4dm = 1040mm (Vì 10,4 × 100 = 1040). b) 5,75cm = 57,5mm (Vì 5,75 × 10 = 57,5) c) 0,856m = 856mm (Vì 0,856 × 1000 = 856). Câu 3 Giải bài toán sau : Một can nhựa chứa 10\(l\) dầu. Biết một lít dầu cân nặng 0,8kg, can rỗng cân nặng 1,3kg. Hỏi can dầu đó cân nặng bao nhiêu ki-lô-gam ? Phương pháp giải: Tóm tắt 1 lít dầu : 0,8kg 1 can rỗng : 1,3kg 10\(l\) dầu và 1 can rỗng : … kg ? - Tìm khối lượng của 10\(l\) dầu. - Tìm khối lượng của can dầu đó. Lời giải chi tiết: 10 lít dầu hỏa nặng số ki-lô-gam là: 0,8 × 10 = 8 (kg) Cả can dầu hỏa nặng số ki-lô-gam là: 8 + 1,3 = 9,3 (kg) Đáp số: 9,3kg. Câu 4 Giải bài toán sau : Một người đi xe đạp, trong hai giờ đầu mỗi giờ đi được 10,8km, trong 3 giờ tiếp theo mỗi giờ đi được 9,52km. Hỏi người đó đã đi được tất cả bao nhiêu ki-lô-mét ? Phương pháp giải: - Tìm quãng đường người đó đi được trong hai giờ đầu. - Tìm quãng đường người đó đi được trong ba giờ tiếp theo. - Tính tổng quãng đường người đó đã đi. Lời giải chi tiết: Hai giờ đầu người đó đi được số ki-lô-mét là : 10,8 × 2 = 21,6 (km) Ba giờ sau người đó đi được số ki-lô-mét là : 9,52 × 3 = 28,56 (km) Vậy, người đó đi được tất cả số ki-lô-mét là : 21,6 + 28,56 = 50,16 (km) Đáp số: 50,16km. Câu 5 Tìm số tự nhiên \(x\), biết: \(2,5 \times x < 7\). Phương pháp giải: - Thực hiện phép nhân \(2,5\) với các số tự nhiên từ \(0, 1, 2, ...\) - So sánh kết quả phép nhân với \(7\) rồi chọn các số thỏa mãn điều kiện bài toán. Lời giải chi tiết: Ta có: \(2,5 \times 0 = 0 < 7\) (thỏa mãn) \(2,5 \times 1 = 2,5 < 7\) (thỏa mãn) \(2,5 \times 2 = 5 < 7\) (thỏa mãn) \(2,5 \times 3 = 7,5 > 7\) (không thỏa mãn) Vậy số tự nhiên \(x\) cần tìm đó là: \(x=0\); \(x= 1\) hoặc \(x= 2\). HocTot.Nam.Name.Vn
|