A. Hoạt động cơ bản - Bài 66 : Rút gọn phân số

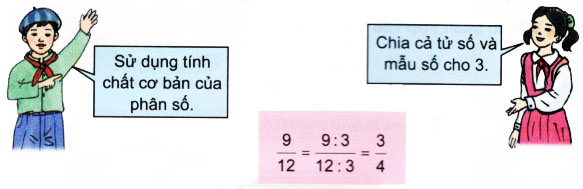
Câu 1

Chơi trò chơi “đố bạn” :

- Em viết một phân số bất kì, chẳng hạn : \(\dfrac{2}{3}\).

- Em đố bạn viết một phân số bằng phân số em vừa viết, chẳng hạn : \(\dfrac{4}{6}\).

- Em và bạn đổi vai cùng chơi.

Phương pháp giải:

Áp dụng tính chất cơ bản của phân số :

- Nếu nhân cả tử số và mẫu số của một phân số với cùng một số tự nhiên khác 0 thì được một phân số bằng phân số đã cho.

- Nếu cả tử số và mẫu số của một phân số cùng chia hết cho một số tự nhiên khác 0 thì sau khi chia ta được một phân số bằng phân số đã cho.

Lời giải chi tiết:

•  \(\dfrac{3}{4}\) bằng với các phân số : \(\dfrac{6}{8}\,\,;\,\,\dfrac{{15}}{{20}}\,\,;\,\,...\)

•  \(\dfrac{4}{7}\) bằng với các phân số : \(\dfrac{{12}}{{21}}\,\,;\,\,\,\dfrac{{20}}{{35}}\,\,;\,\,...\)

•  \(\dfrac{5}{8}\) bằng với các phân số : \(\dfrac{{20}}{{32}}\,\,;\,\,\,\dfrac{{35}}{{56}}\,\,;\,\,...\)

Câu 2

Thực hiện lần lượt các hoạt động :

a) Tìm phân số bằng phân số \(\dfrac{9}{{12}}\) nhưng có tử số và mẫu số bé hơn :

b) Đọc kĩ nội dung sau và nói với bạn :

Nhận xét :

\(\dfrac{9}{{12}} = \dfrac{3}{4}.\)

Tử số và mẫu số của phân số \(\dfrac{3}{4}\) đều bé hơn tử số và mẫu số của phân số \(\dfrac{9}{{12}}\).

Ta nói rằng : Phân số \(\dfrac{9}{{12}}\) đã được rút gọn thành phân số \(\dfrac{3}{4}\).

c) Đọc và thực hiện từng bước cách rút gọn phân số trong các ví dụ sau :

Ví dụ 1: Rút gọn phân số \(\dfrac{4}{6}\).

Ta thấy 4 và 6 đều chia hết cho 2, nên \(\dfrac{4}{6}=\dfrac{4:2}{6:2}=\dfrac{2}{3}\). 

2 và 3 không cùng chia hết cho một số tự nhiên nào lớn hơn 1, nên phân số \(\dfrac{2}{3}\) không thể rút gọn được nữa.

Ta nói rằng : Phân số \(\dfrac{2}{3}\) là phân số tối giản. Phân số \(\dfrac{4}{6}\) đã được rút gọn thành phân số tối giản \(\dfrac{2}{3}\).

Ví dụ 2: Rút gọn phân số \(\dfrac{18}{24}\).

Ta thấy :  18 và 24 đều chia hết cho 2, nên \(\dfrac{18}{24}=\dfrac{18:2}{24:2}=\dfrac{9}{12}\).

9 và 12 đều chia hết cho 3, nên \(\dfrac{9}{12}=\dfrac{9:3}{12:3}=\dfrac{3}{4}\).

3 và 4 không cùng chia hết cho một số tự nhiên nào lớn hơn 1, nên \(\dfrac{3}{4}\)  là phân số tối giản.

Vậy : \(\dfrac{{18}}{{24}} = \dfrac{3}{4}.\)

Lời giải chi tiết:

a) Em sử dụng tính chất cơ bản của phân số: Lấy cả tử số và mẫu số của phân số đã cho chia cho 3.

Tử số: Lấy 9 chia cho 3 được 3.

Mẫu số: Lấy 12 chia cho 3 được 4.

Phân số \(\dfrac{9}{12}=\dfrac{3}{4}\)

b) Em đọc kĩ nội dung trong sách và nói với bạn của mình.

c) Em đọc và thực hiện từng bước cách rút gọn phân số trong các ví dụ.

Câu 3

a) Đọc kĩ nhận xét sau và nghe thầy/ cô giáo hướng dẫn :

b) Rút gọn các phân số sau : \(\dfrac{2}{6}\,\,;\,\,\,\,\,\,\,\dfrac{{12}}{{36}}.\)

Phương pháp giải:

Khi rút gọn phân số ta có thể làm như sau :

• Xét xem tử số và mẫu số cùng chia hết cho số tự nhiên nào lớn hơn 1.

• Chia cả tử số và mẫu số cho số đó.                 

Cứ làm như thế cho đến khi nhận được phân số tối giản.

Lời giải chi tiết:

\(\dfrac{2}{6} = \dfrac{{2:2}}{{6:2}} = \dfrac{1}{3}\,\,;\,\,\,\,\,\,\)                 \(\dfrac{{12}}{{36}} = \dfrac{{12:12}}{{36:12}} = \dfrac{1}{3}.\)

 HocTot.Nam.Name.Vn