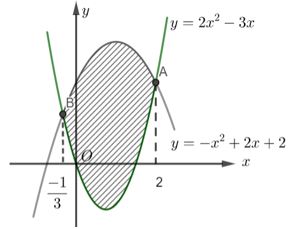
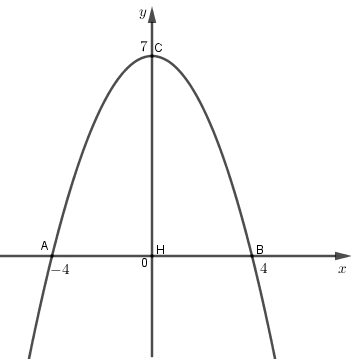
Giải đề thi học kì 2 toán lớp 12 năm 2019 - 2020 Sở GD&ĐT Đà Nẵng

Câu 1. Trong không gian \(Oxyz,\) mặt phẳng \(\left( P \right):2x - 3y + z - 7 = 0\) có một vectơ pháp tuyến là

A. \(\overrightarrow {{n_1}}  = \left( {2;3; - 1} \right).\)

B. \(\overrightarrow {{n_2}}  = \left( {1;3;2} \right).\)

C. \(\overrightarrow {{n_3}}  = \left( {2; - 3;1} \right).\)

D. \(\overrightarrow {{n_4}}  = \left( { - 1;3;2} \right).\)

Câu 2. Giả sử \(\int\limits_1^2 {\left( {1 - \frac{4}{x}} \right){\rm{d}}x}  = a + b\ln 2\) với a, b là các số nguyên. Khi đó \(a - b\) bằng

A. \( - 3\).                               B. \(3\).

C. \(5\).                                  D. \( - 5.\)

Câu 3. Cho hai số phức \({z_1} = 15 - 6i\) và \({z_2} = 7 - 6i\). Tìm số phức \(z = {z_1} + {z_2}\).

A. \(z = 22.\)

B. \(z = 22 - 12i.\)

C. \(z = 8 - 12i.\)

D. \(z = 22 + 12i.\)

Câu 4. Cho số phức \(z = a + bi,\) với \(a,b \in \mathbb{R}\). Tìm mệnh đề đúng.

A. \(\left| z \right| = \sqrt {{a^2} + {b^2}} .\)

B. \(\left| z \right| = {a^2} + {b^2}.\)

C. \(\left| z \right| = \left| {a + b} \right|.\)

D. \(\left| z \right| = \left| a \right| + \left| b \right|.\)

Câu 5. Trong không gian \(Oxyz,\) phương trình mặt phẳng đi qua ba điểm \(A(0;3;0),B(2;0;0),C(0;0;4)\) là

A. \(\frac{x}{2} + \frac{y}{3} + \frac{z}{4} = 1.\)

B. \(\frac{x}{3} + \frac{y}{2} + \frac{z}{4} = 1.\)

C. \(\frac{x}{3} + \frac{y}{2} + \frac{z}{4} = 0.\)

D. \(\frac{x}{2} + \frac{y}{3} + \frac{z}{4} = 0.\)

Câu 6. Cho số phức \(z = 15 - 6i\). Khi đó \(z + \bar z\) bằng

A. \(30.\)                                B. \( - 12i.\)

C. \(0.\)                                  D. \(261.\)

Câu 7. Cho hàm số \(f\left( x \right)\) thỏa mãn \(\int\limits_1^3 {f\left( x \right)} \,{\rm{d}}x = 22\) và \(\int\limits_{ - 1}^3 {f\left( x \right)\,} {\rm{d}}x = 24\). Tính \(I = \int\limits_{ - 1}^1 {f\left( x \right)} \,{\rm{d}}x.\)

A. \(I = 46.\)                          B. \(I =  - 46.\)

C. \(I =  - 2.\)                         D. \(I = 2.\)

Câu 8. Tính \(I = \int\limits_0^{\frac{\pi }{3}} {\left( {3x - 1} \right)\sin 3x{\rm{d}}x} \) bằng phương pháp tính tích phân từng phần, đặt \(u = 3x - 1\) và \({\rm{d}}v = \sin 3x{\rm{d}}x\). Khi đó:

A. \(I = \left. {\left( {1 - 3x} \right)\cos 3x} \right|_0^{\frac{\pi }{3}} + \int\limits_0^{\frac{\pi }{3}} {\cos 3x{\rm{d}}x} .\)

B. \(I = \frac{1}{3}\left. {\left( {3x - 1} \right)\cos 3x} \right|_0^{\frac{\pi }{3}} + \int\limits_0^{\frac{\pi }{3}} {\cos 3x{\rm{d}}x} .\)

C. \(I = \left. {\left( {1 - 3x} \right)\cos 3x} \right|_0^{\frac{\pi }{3}} - \int\limits_0^{\frac{\pi }{3}} {\cos 3x{\rm{d}}x} .\)

D. \(I = \frac{1}{3}\left. {\left( {1 - 3x} \right)\cos 3x} \right|_0^{\frac{\pi }{3}} + \int\limits_0^{\frac{\pi }{3}} {\cos 3x{\rm{d}}x} .\)

Câu 9. Số phức \(z = 6 + 7i\) được biểu diễn trên mặt phẳng tọa độ bởi điểm:

A. \(M\left( {6; - 7} \right).\)                                          B. \(Q\left( {6;7} \right).\)

C. \(P\left( { - 6;7} \right).\) D. \(N\left( { - 6; - 7} \right).\)

Câu 10. Tính \(P = (3 + 2i)( - 4 + 5i) - 7i\).

A. \(P = 15.\)                          B. \(P = 5.\)

C. \(P =  - 22.\)                      D. \(P = 7.\)

Câu 11. Trong không gian \(Oxyz,\) phương trình tham số của đường thẳng đi qua điểm \(I\left( {2;0; - 3} \right)\)và có vectơ chỉ phương \(\overrightarrow u  = \left( { - 5;4;3} \right)\) là

A. \(\left\{ \begin{array}{l}x = 2 - 5t\\y = 0\\z =  - 3 + 3t.\end{array} \right.\)

B. \(\left\{ \begin{array}{l}x =  - 5 + 2t\\y = 4\\z = 3 - 3t.\end{array} \right.\)

C. \(\left\{ \begin{array}{l}x = 2 + 5t\\y = 4t\\z =  - 3 + 3t.\end{array} \right.\)

D. \(\left\{ \begin{array}{l}x = 2 - 5t\\y = 4t\\z =  - 3 + 3t.\end{array} \right.\)

Câu 12. Trong không gian \(Oxyz\), tìm tọa độ của \(\overrightarrow x  = \vec i - 5\vec j + 7\vec k.\)

A. \(\overrightarrow x  = (1; - 5;7).\)

B. \(\overrightarrow x  = (1;5;7).\)

C. \(\overrightarrow x  = (1;5; - 7).\)

D. \(\overrightarrow x  = (0; - 5;7).\)

Câu 13. Xét \(\int\limits_0^{\sqrt 2 } {\frac{1}{{\sqrt {4 - {x^2}} }}{\rm{d}}x} \), nếu đặt \(x = 2\sin t,\) với \(t \in \left[ {\frac{{ - \pi }}{2};\frac{\pi }{2}} \right]\) thì \(\int\limits_0^{\sqrt 2 } {\frac{1}{{\sqrt {4 - {x^2}} }}{\rm{d}}x} \) bằng

A. \(\int\limits_0^{\frac{\pi }{4}} {\cos t{\rm{d}}t} .\)

B. \(\int\limits_0^{\frac{\pi }{4}} {\sin t{\rm{d}}t} .\)

C. \(\frac{1}{4}\int\limits_0^{\frac{\pi }{4}} {{\rm{d}}t} .\)

D. \(\int\limits_0^{\frac{\pi }{4}} {{\rm{d}}t} .\)

Câu 14. Trong không gian \(Oxyz,\) phương trình nào dưới đây là phương trình của mặt phẳng (Oxz) ?

A. \(x + z = 0.\)                      B. \(x = 0.\)

C. \(z = 0.\)                            D. \(y = 0.\)

Câu 15. Trong không gian \(Oxyz\), hình chiếu vuông góc của điểm \(A\left( {2; - 4;3} \right)\) trên mặt phẳng \(\left( {Oxz} \right)\) là điểm

A. \(P\left( {2;0;3} \right).\)

B. \(N\left( {2; - 4;0} \right).\)

C. \(M\left( {0; - 4;3} \right).\)

D. \(Q\left( {0; - 4;0} \right).\)

Câu 16. Cho \(I = \int\limits_0^{2\sqrt 2 } {2x\sqrt {{x^2} + 1} \,} {\rm{d}}x\) và đặt \(u = \sqrt {{x^2} + 1} \). Chọn mệnh đề sai.

A. \(I = \left. {\frac{{2{u^3}}}{3}} \right|_1^3.\)

B. \(I = \int\limits_1^3 {2{u^2}} {\rm{d}}u.\)

C. \(I = \int\limits_1^3 {2u} {\rm{d}}u.\)

D. \(I = \frac{{52}}{3} \cdot \)

Câu 17. Số phức \(1 - 3i\) có phần thực và phần ảo lần lượt là

A. 1 và \( - 3.\)                       B. 1 và \( - 3i.\)

C. 1 và 3.                               D. \( - 3\) và 1.

Câu 18. Cho số phức \(z.\) Tìm mệnh đề đúng.

A. \(z.\bar z = {\left| z \right|^2}.\)

B. \(z.\bar z = \left| z \right|.\)

C. \(z.\bar z = {z^2}.\)

D. \(z.\bar z = {\bar z^2}.\)

Câu 19.  \(\int\limits_1^3 {\frac{{{\rm{d}}x}}{{3x + 1}}} \) bằng

A.  \(\ln \frac{5}{2} \cdot \)  B. \(3\ln \frac{5}{2} \cdot \)

C. \(\frac{1}{3}\ln \frac{5}{2} \cdot \)                          D. \(\frac{1}{3}\ln 40.\)

Câu 20. \(\int\limits_0^3 {({e^x}{\rm{ + 1)d}}x} \) bằng

A. \(e + 2\).                            B. \(e - 1\).

C. \({e^3} + 1\).                     D. \({e^3} + 2.\)

Câu 21. Cho hàm số \(y = f\left( x \right)\) liên tục trên đoạn \(\left[ {a;\,b} \right]\). Diện tích \(S\) của hình phẳng giới hạn bởi đồ thị hàm số \(y = f\left( x \right)\), trục hoành và hai đường thẳng \(x = a\), \(x = b\) được tính theo công thức:

A. \(S =  - \int\limits_a^b {f\left( x \right)\,{\rm{d}}x} .\)

B. \(S = \left| {\int\limits_a^b {f\left( x \right)\,{\rm{d}}x} } \right|.\)

C. \(S = \int\limits_a^b {\left| {f\left( x \right)} \right|\,{\rm{d}}x} .\)

D. \(S = \int\limits_a^b {\,f\left( x \right){\rm{d}}x} .\)

Câu 22. Trong không gian \(Oxyz\), cho hai điểm \(A\left( {1;\,1;\, - 2} \right)\) và \(B\left( {2;\, - 2;\,1} \right)\). Khi đó \(\overrightarrow {AB} \) có tọa độ là:

A. \(\left( {3;\,3;\, - 1} \right)\).

B. \(\left( { - 1;\,3;\, - 3} \right)\).

C. \(\left( {3;\,1;\,1} \right)\).

D. \(\left( {1;\, - 3;\,3} \right)\).

Câu 23. Cho hình phẳng \(\left( H \right)\) giới hạn bởi các đường \(y = {x^2} + 5,\,y = 0,\,x = 1\) và \(x = 3.\) Gọi \(V\) là thể tích của khối tròn xoay được tạo thành khi quay \(\left( H \right)\)xung quanh trục \(Ox.\) Khi đó

A. \(V = \int\limits_1^3 {\left( {{x^2} + 5} \right){\rm{d}}x} \).

B. \(V = \int\limits_1^3 {{{\left( {{x^2} + 5} \right)}^2}{\rm{d}}x} \).

C. \(V = \pi \int\limits_1^3 {\left( {{x^2} + 5} \right){\rm{d}}x} \).

D. \(V = \pi \int\limits_1^3 {{{\left( {{x^2} + 5} \right)}^2}{\rm{d}}x} \).

Câu 24. Trong không gian \(Oxyz\), khoảng cách từ điểm \(A(1; - 2;3)\) đến mặt phẳng \((P):\,\,x + 4y - 2z - 6 = 0\) bằng

A. \(\frac{{19}}{{21}} \cdot \)                                        B. \(\frac{{19\sqrt {21} }}{{21}} \cdot \)

C. \(\frac{{\sqrt {21} }}{{21}} \cdot \)                          D. \(\frac{{21}}{{19}} \cdot \)

Câu 25. Trong không gian \(Oxyz,\) đường thẳng \(d:\frac{{x + 7}}{2} = \frac{{y - 8}}{{ - 2}} = \frac{{z - 9}}{{ - 3}}\) có một vectơ chỉ phương là

A. \(\overrightarrow {{u_1}}  = \left( { - 7;8;9} \right).\)

B. \(\overrightarrow {{u_4}}  = \left( {7; - 8; - 9} \right).\)

C. \(\overrightarrow {{u_3}}  = \left( {2;2;3} \right).\)

D. \(\overrightarrow {{u_2}}  = \left( {2; - 2; - 3} \right).\)

Câu 26. Gọi \(S\) là diện tích của hình phẳng giới hạn bởi các đường \(y = {7^x}\), \(y = 0\), \(x = 0\), \(x = 2\). Khi đó:

A. \(S = \pi \int\limits_0^2 {{7^x}{\rm{d}}x} \).

B. \(S = \pi \int\limits_0^2 {{7^{2x}}{\rm{d}}x} \).

C. \(S = \int\limits_0^2 {{7^{2x}}{\rm{d}}x} \).

D. \(S = \int\limits_0^2 {{7^x}{\rm{d}}x} \).

Câu 27. Số phức liên hợp của số phức \(z = 3i - 5\) là

A. \(\bar z =  - 5 + 3i.\)

B. \(\bar z = 3i + 5.\)

C. \(\bar z =  - 5 - 3i.\)

D. \(\bar z = 5 - 3i.\)

Câu 28. Diện tích phần hình phẳng được gạch chéo trong hình bên bằng

A. \(\int\limits_{ - \frac{1}{3}}^2 {\left( { - 3{x^2} + 5x + 2} \right)\,{\rm{d}}x} .\)

B. \(\int\limits_{ - \frac{1}{3}}^2 {\left( {3{x^2} - 5x - 2} \right)\,{\rm{d}}x} .\)

C. \(\int\limits_{ - \frac{1}{3}}^2 {\left( { - {x^2} + x + 2} \right)\,{\rm{d}}x} .\)

D. \(\int\limits_{ - \frac{1}{3}}^2 {\left( {{x^2} - 5x + 2} \right)\,{\rm{d}}x} .\)

Câu 29. Trên mặt phẳng tọa độ, tập hợp các điểm biểu diễn các số phức z thỏa mãn điều kiện \(\left| z \right| = 2\) là

A. đường tròn tâm \(O(0;0),\)bán kính bằng 1.

B. đường tròn tâm \(I(2;2),\)bán kính bằng \(\sqrt 2 .\)

C. đường tròn tâm \(O(0;0),\)bán kính bằng \(4.\)

D. đường tròn tâm \(O(0;0),\)bán kính bằng \(2.\)

Câu 30. Trong không gian \(Oxyz\), mặt phẳng qua ba điểm \(A\left( {1;1;1} \right),B\left( {0;2;3} \right),C\left( { - 2;0;1} \right)\) có một vectơ pháp tuyến là

A. \(\overrightarrow {{n_1}}  = \left( {2;6;4} \right).\)

B. \(\overrightarrow {{n_4}}  = \left( {2;6; - 4} \right).\)

C. \(\overrightarrow {{n_3}}  = \left( {1; - 3; - 2} \right).\)

D. \(\overrightarrow {{n_2}}  = \left( {1; - 3;2} \right).\)

Câu 31. Trong không gian \(Oxyz\), cho ba vectơ \(\overrightarrow a  = ( - 2; - 5;0),\) \(\overrightarrow b  = \left( {1;2;1} \right),\) \(\overrightarrow c  = \left( {2;3;2} \right)\). Tọa độ \(\overrightarrow d  = 3\overrightarrow a  - \overrightarrow b  - 2\overrightarrow c \) là:

A. \(\left( {5;27;3} \right)\).

B. \(\left( { - 1; - 2;5} \right).\)

C. \(\left( {0;27;3} \right)\).

D. \(( - 11; - 23; - 5).\)

Câu 32. Cho số phức \(z = a + bi,{\mkern 1mu} {\mkern 1mu} \,\,\left( {a,b \in \mathbb{R}} \right)\) thỏa mãn \(\left( {1 + 3i} \right)z + 5\,\bar z = 4 - i.\) Tính \(P = a + b\).

A. \(P = \frac{1}{{15}} \cdot \)                                      B. \(P = \frac{7}{{15}} \cdot \)

C. \(P =  - \frac{{37}}{{15}} \cdot \)                              D. \(P = \frac{{37}}{{15}} \cdot \)

Câu 33. Trong không gian \(Oxyz\), cho điểm \(I\left( {2;1;3} \right)\) và \(A\left( { - 1;3;0} \right).\) Phương trình của mặt cầu có tâm \(I\) và đi qua điểm \(A\) là

A. \({\left( {x - 2} \right)^2} + {\left( {y - 1} \right)^2} + {\left( {z - 3} \right)^2} = 44.\)

B. \({\left( {x + 1} \right)^2} + {\left( {y - 3} \right)^2} + {z^2} = 44.\)

C. \({\left( {x + 1} \right)^2} + {\left( {y - 3} \right)^2} + {z^2} = 22.\)

D. \({\left( {x - 2} \right)^2} + {\left( {y - 1} \right)^2} + {\left( {z - 3} \right)^2} = 22.\)

Câu 34. Trong không gian Oxyz, viết phương trình mặt phẳng qua điểm \(M\left( {1;2;1} \right)\) và cắt các trục tọa độ \(Ox,Oy,Oz\) lần lượt tại các điểm \(I,K,H\) sao cho tam giác \(IKH\) có trực tâm là \(M.\)

A. \(x + 2y + 3z - 8 = 0.\)

B. \(3x + y - z - 4 = 0.\)

C. \(x + 2y + z - 6 = 0.\)

D. \(2x + 4y + 2z - 9 = 0.\)

Câu 35. Cho \(\int\limits_0^1 {f\left( {ex} \right){\rm{d}}x}  = 1\), khi đó \(\int\limits_0^e {\left[ {f\left( x \right) - e} \right]{\rm{d}}x} \) bằng

A. \(e - {e^e}.\)                      B. \({e^2} - e.\)

C. \(2e.\)                                 D. \(e - {e^2}.\)

Câu 36. Cho hàm số \(f\left( x \right)\) có đạo hàm liên tục trên \(\mathbb{R}\) thỏa mãn \(\int\limits_0^1 {xf'\left( x \right){\rm{d}}x}  = m\) và \(f\left( 1 \right) = 3.\) Khi đó \(\int\limits_0^1 {f\left( x \right){\rm{d}}x} \) bằng

A. \(m - 3.\)                            B. \(m + 3.\)

C. \(3 - m.\)                            D. \( - m - 3.\)

Câu 37. Trong không gian \(Oxyz\), cho điểm \(A\left( {2;\,1;\,3} \right)\) và đường thẳng \(d:\frac{{x + 1}}{1} = \frac{{y - 1}}{{ - 2}} = \frac{{z - 2}}{2} \cdot \) Đường thẳng đi qua \(A\), vuông góc với \(d\) và cắt trục \(Oy\) có phương trình là

A. \(\frac{x}{2} = \frac{{y + 3}}{4} = \frac{z}{3} \cdot \)

B. \(\frac{{x - 2}}{2} = \frac{{y - 1}}{1} = \frac{{z - 3}}{3} \cdot \)

C. \(\frac{{x - 2}}{2} = \frac{{y - 1}}{3} = \frac{{z - 3}}{2} \cdot \)

D. \(\frac{x}{2} = \frac{{y + 3}}{3} = \frac{z}{2} \cdot \)

Câu 38. Tìm các số thực \(x,y\) thỏa mãn: \(\left( {x + y} \right) + \left( {2x - y} \right)i = 3 - 6i,\) với i là đơn vị ảo.

A. \(x =  - 1;y =  - 4.\)

B. \(x = 1;y =  - 4.\)

C. \(x = 4;y =  - 1.\)

D. \(x =  - 1;y = 4.\)

Câu 39. Tìm số phức liên hợp của số phức \(z = 3i\left( {i - 4} \right)\).

A. \(\bar z =  - 3 - 12i.\)

B. \(\bar z =  - 12 + 3i.\)

C. \(\bar z = 12 + 3i.\)

D. \(\bar z =  - 3 + 12i.\)

Câu 40. Cho hàm số \(f\left( x \right)\) có đạo hàm liên tục trên đoạn \(\left[ {1;4} \right]\), thỏa mãn\(f(4) = 15\) và \(\int\limits_1^4 {f'(x){\rm{d}}x = 19} .\) Tính \(f(1).\)

A. \(f(1) =  - 4.\)                     B. \(f(1) = 4.\)

C. \(f(1) = 34.\)                      D. \(f(1) =  - 34.\)

Câu 41. Diện tích hình phẳng giới hạn bởi đồ thị hàm số \(y = \ln x\), trục hoành và đường thẳng \(x = e\) là

A. 2.                                       B. 5.

C. 3.                                       D. 1.

Câu 42. Thể tích khối tròn xoay do hình phẳng giới hạn bởi các đường \(y = \frac{{{x^2} + x + 1}}{{x + 1}},\) \(y = 0,\) \(x = 0,\) \(x = 1\) quay quanh trục \(Ox\) là

A. \(\pi \left( {\frac{{15}}{6} + 2\ln 2} \right).\)

B. \(\pi \left( {\frac{{17}}{6} - 2\ln 2} \right).\)

C. \(\pi \left( {\frac{3}{2} + \ln 2} \right).\)

D. \(\pi \left( {\frac{{17}}{2} + \ln 2} \right).\)

Câu 43. Xét các số phức z thỏa mãn điều kiện \(\left| {z - 1 + 3i} \right| = \left| {z - 2i} \right|\). Giá trị nhỏ nhất của \(\left| z \right|\) là

A. \(\frac{{3\sqrt {26} }}{{26}} \cdot \)

B. \(\frac{{\sqrt {26} }}{{13}} \cdot \)

C. \(\frac{{\sqrt {26} }}{{26}} \cdot \)

D. \(\frac{{3\sqrt {26} }}{{13}} \cdot \)

Câu 44. Trong không gian \(Oxyz\), cho các điểm \(A(6;0;0),B(0;0;6),C(0;6;6).\) Xét các điểm \(M,N\) di chuyển trên các đoạn \(AB\)và \(OC\) sao cho \(AM = ON.\) Khi độ dài đoạn thẳng \(MN\) nhỏ nhất, phương trình đường thẳng \(MN\) là

A. \(\left\{ \begin{array}{l}x = t\\y = 0\\z = 0.\end{array} \right.\)

B. \(\left\{ \begin{array}{l}x = 2 - t\\y = t\\z = 4 - t.\end{array} \right.\)

C. \(\left\{ \begin{array}{l}x = 3 + t\\y =  - t\\z = 3.\end{array} \right.\)

D. \(\left\{ \begin{array}{l}x = 0\\y = t\\z = 6.\end{array} \right.\)

Câu 45. Vòm cửa lớn của một trung tâm thương mại có dạng parabol như hình vẽ, trong đó khoảng cách \(AB = 8\,{\rm{m}}\) và chiều cao của vòm cửa là \(CH = 7\,{\rm{m}}.\) Người ta cần ốp kính cho toàn bộ vòm cửa này, khi đó diện tích kính cần dùng ít nhất là:

A. \(\frac{{115}}{3}{{\rm{m}}^2}.\)  B. \(\frac{{120}}{3}{{\rm{m}}^2}.\)

C. \(\frac{{110}}{3}{{\rm{m}}^2}.\)  D. \(\frac{{112}}{3}{{\rm{m}}^2}.\)

Câu 46. Cho hàm số \(y = f\left( x \right)\) có \(f\left( 1 \right) = \frac{1}{6}\) và \(f\prime \left( x \right) = \frac{{ - 2x - 3}}{{{{\left( {{x^2} + 3x + 2} \right)}^2}}}\), \(\forall x \ge 0\). Khi đó \(\int\limits_0^1 {f\left( x \right){\rm{d}}x} \) bằng

A. \( - \frac{1}{3} \cdot \)     B. \(\ln \frac{2}{3} \cdot \)

C. \(\ln \frac{4}{3} \cdot \)   D. \( - \frac{1}{2} \cdot \)

Câu 47. Có tất cả bao nhiêu giá trị của tham số thực \(m \in \left( {0;2020} \right]\) để \(\int\limits_0^m {\sin 2x\sqrt {1 + {{\sin }^2}x} {\rm{d}}x = 0} ?\)

A. 643.                                   B. 2020.

C. 642.                                   D. 2019.

Câu 48. Trong không gian Oxyz, cho điểm \(A\left( {2;0;0} \right)\) và mặt phẳng \(\left( P \right):3y - 3z + 7 = 0.\) Trên các tia Oy, Oz lần lượt lấy các điểm \(B,C\) phân biệt sao cho mặt phẳng \(\left( {ABC} \right)\) vuông góc với mặt phẳng \(\left( P \right)\) và khoảng cách từ gốc tọa độ \(O\) đến mặt phẳng \(\left( {ABC} \right)\) bằng \(\sqrt 2 .\) Xác định tọa độ điểm B và điểm \(C.\)

A. \(B\left( {0;2\sqrt 2 ;0} \right),C\left( {0;0;2\sqrt 2 } \right).\)

B. \(B\left( {0;4;0} \right),C\left( {0;0;4} \right).\)

C. \(B\left( {0;2\sqrt 6 ;0} \right),C\left( {0;0;2\sqrt 6 } \right).\)

D. \(B\left( {0;16;0} \right),C\left( {0;0;16} \right).\)

Câu 49. Cho các số phức \({z_1},{z_2}\) thỏa mãn \(\left| {{z_1}} \right| = 2\left| {{z_2}} \right| = 4\) và \(\left| {{z_1} - {z_2}} \right| = 3.\)Tính \(\left| {{z_1} + {z_2}} \right|.\)

A. \(\left| {{z_1} + {z_2}} \right| = \sqrt 6 .\)

B. \(\left| {{z_1} + {z_2}} \right| = \frac{{\sqrt {31} }}{2} \cdot \)

C. \(\left| {{z_1} + {z_2}} \right| = 6.\)

D. \(\left| {{z_1} + {z_2}} \right| = \sqrt {31} .\)

Câu 50. Trong không gian \(Oxyz,\) cho ba điểm \(A(1;0;0),\,B(3;2;4),\,C(0;5;4)\). Gọi \(M(a;b;c)\) là điểm thuộc mặt phẳng \((Oyz)\)sao cho biểu thức \(T = M{A^2} + M{B^2} + 2M{C^2}\) đạt giá trị nhỏ nhất. Khi đó \(a + b + c\)bằng

A. 0.                                       B. 6.

C. 5.                                       D. 2.

-- Hết --

ĐÁP ÁN

HƯỚNG DẪN GIẢI CHI TIẾT

Thực hiện: Ban chuyên môn HocTot.Nam.Name.Vn

Câu 1:

Phương pháp:

Sử dụng: Mặt phẳng \(\left( P \right):ax + by + cz + d = 0\) có 1 VTPT \(\overrightarrow n  = \left( {a;b;c} \right)\)

Hướng dẫn giải:

Ta có mặt phẳng \(\left( P \right):2x - 3y + z - 7 = 0\) có một vectơ pháp tuyến là \(\overrightarrow n  = \left( {2; - 3;1} \right)\)

Đáp án C

Câu 2:

Phương pháp:

Sử dụng: \(\int\limits_a^b {f\left( x \right)dx}  = \left. {F\left( x \right)} \right|_a^b\) \( = F\left( b \right) - F\left( a \right)\)  với \(F\left( x \right)\) là một nguyên hàm của hàm số \(f\left( x \right).\)

Hướng dẫn giải:

Ta có \(\int\limits_1^2 {\left( {1 - \frac{4}{x}} \right){\rm{d}}x}  = \left. {\left( {x - 4\ln \left| x \right|} \right)} \right|_1^2\)\( = 2 - 4\ln 2 - \left( {1 - 4\ln 1} \right)\)\( = 1 - 4\ln 2\)

Suy ra \(a = 1;b =  - 4\) nên \(a - b = 1 - \left( { - 4} \right) = 5\)

Đáp án C

Câu 3:

Phương pháp:

Sử dụng: Với \({z_1} = {a_1} + {b_1}i;{z_2} = {a_2} + {b_2}i\) (\({a_1};{a_2};{b_1};{b_2} \in \mathbb{R}\)) thì \({z_1} + {z_2} = \left( {{a_1} + {a_2}} \right) + \left( {{b_1} + {b_2}} \right)i\)

Hướng dẫn giải:

Ta có \(z = {z_1} + {z_2}\)\( = 15 - 6i + 7 - 6i = 22 - 12i\)

Đáp án B

Câu 4:

Phương pháp:

Cho số phức \(z = a + bi\left( {a,b \in \mathbb{R}} \right)\) thì mô đun \(\left| z \right| = \sqrt {{a^2} + {b^2}} \)

Hướng dẫn giải:

Ta có \(\left| z \right| = \sqrt {{a^2} + {b^2}} \)

Đáp án A

Câu 5:

Phương pháp:

Mặt phẳng đi qua ba điểm \(A\left( {a;0;0} \right),B\left( {0;b;0} \right),C\left( {0;0;c} \right)\) với \(abc \ne 0\) có phương trình \(\frac{x}{a} + \frac{y}{b} + \frac{z}{c} = 1\)

Hướng dẫn giải:

Phương trình mặt phẳng cần tìm là \(\frac{x}{2} + \frac{y}{3} + \frac{z}{4} = 1\)

Đáp án A

Câu 6:

Phương pháp:

Cho số phức \(z = a + bi\left( {a,b \in \mathbb{R}} \right)\) thì \(\overline z  = a - bi\)

Muốn cộng hai số phức ta cộng phần thực với nhau, phần ảo với nhau

Hướng dẫn giải:

Ta có \(\overline z  = 15 + 6i\)

Nên \(z + \overline z  = 15 - 6i + 15 + 6i\) \( = 30\)

Đáp án A

Câu 7:

Phương pháp:

Sử dụng: \(\int\limits_a^b {f\left( x \right)} dx = \int\limits_a^c {f\left( x \right)} dx + \int\limits_c^a {f\left( x \right)} dx\)

Hướng dẫn giải:

Ta có \(\int\limits_1^3 {f\left( x \right)} \,{\rm{d}}x = 22\)\( \Leftrightarrow \int\limits_3^1 {f\left( x \right)} \,{\rm{d}}x =  - 22\)

Suy ra \(\int\limits_{ - 1}^3 {f\left( x \right)} \,{\rm{d}}x + \int\limits_3^1 {f\left( x \right)} \,{\rm{d}}x\) \( = 24 + \left( { - 22} \right) = 2\)

Đáp án D

Câu 8:

Phương pháp:

Sử dụng phương pháp tính tích phân từng phần

Hướng dẫn giải:

Ta có \(I = \int\limits_0^{\frac{\pi }{3}} {\left( {3x - 1} \right)\sin 3x{\rm{d}}x} \)

Đặt \(\left\{ \begin{array}{l}u = 3x - 1\\\sin 3xdx = dv\end{array} \right.\) \( \Rightarrow \left\{ \begin{array}{l}du = 3dx\\v =  - \frac{1}{3}\cos 3x\end{array} \right.\)

Suy ra \(I = \int\limits_0^{\frac{\pi }{3}} {\left( {3x - 1} \right)\sin 3x{\rm{d}}x} \)\( =  - \left. {\frac{1}{3}\left( {3x - 1} \right)\cos 3x} \right|_0^{\frac{\pi }{3}} + \int\limits_0^{\frac{\pi }{3}} {\cos 3xdx} \) \( = \left. {\frac{1}{3}\left( {1 - 3x} \right)\cos 3x} \right|_0^{\frac{\pi }{3}} + \int\limits_0^{\frac{\pi }{3}} {\cos 3xdx} \)

Đáp án D

Câu 9:

Phương pháp:

Sử dụng: Số phức \(z = a + bi\) được biểu diễn bởi điểm \(M\left( {a;b} \right)\)

Hướng dẫn giải:

Ta có số phức \(z = 6 + 7i\) được biểu diễn trên mặt phẳng tọa độ bởi điểm \(Q\left( {6;7} \right).\)

Đáp án B

Câu 10:

Phương pháp:

Tính toán nhân chia, cộng trừ số phức với lưu ý \({i^2} =  - 1\)

Hướng dẫn giải:

Ta có:

\(\begin{array}{l}P = (3 + 2i)( - 4 + 5i) - 7i\\ =  - 12 + 15i - 8i + 10{i^2} - 7i\\ =  - 12 + 7i - 10 - 7i\\ =  - 22\end{array}\)

Đáp án C

Câu 11:

Phương pháp:

Sử dụng: Phương trình đường thẳng đi qua \(M\left( {{x_0};{y_0};{z_0}} \right)\) và có VTCP \(\overrightarrow u  = \left( {a;b;c} \right)\) là: \(\left\{ \begin{array}{l}x = {x_0} + at\\y = {y_0} + bt\\z = {z_0} + ct\end{array} \right.\)

Hướng dẫn giải:

Phương trình cần tìm là  \(\left\{ \begin{array}{l}x = 2 - 5t\\y = 4t\\z =  - 3 + 3t.\end{array} \right.\)

Đáp án D

Câu 12:

Phương pháp:

Sử dụng: \(\overrightarrow u  = a\overrightarrow i  + b\overrightarrow j  + c\overrightarrow k \) thì \(\overrightarrow u  = \left( {a;b;c} \right)\)

Hướng dẫn giải:

Ta có \(\overrightarrow x  = \vec i - 5\vec j + 7\vec k\)\( \Rightarrow \overrightarrow x  = \left( {1; - 5;7} \right)\)

Đáp án A

Câu 13:

Phương pháp:

Sử dụng phương pháp đổi biến số để tính tích phân

Hướng dẫn giải:

Đặt \(x = 2\sin t \Rightarrow dx = 2\cos tdt\)

Đổi cận: Với \(x = 0 \Rightarrow \sin t = 0\) \( \Rightarrow t = 0\)

Với \(x = \sqrt 2  \Rightarrow \sin t = \frac{{\sqrt 2 }}{2}\) \( \Rightarrow t = \frac{\pi }{4}\)

Ta có:  \(\int\limits_0^{\sqrt 2 } {\frac{1}{{\sqrt {4 - {x^2}} }}{\rm{d}}x} \)\( = \int\limits_0^{\frac{\pi }{4}} {\frac{1}{{\sqrt {4 - {{\left( {2\sin t} \right)}^2}} }}.2\cos tdt} \)

\(\begin{array}{l} = \int\limits_0^{\frac{\pi }{4}} {\frac{1}{{\sqrt {4\left( {1 - {{\sin }^2}t} \right)} }}} 2\cos tdt\\ = \int\limits_0^{\frac{\pi }{4}} {\frac{1}{{2\cos t}}.2\cos tdt}  = \int\limits_0^{\frac{\pi }{4}} {dt} \end{array}\)

Đáp án D

Câu 14:

Phương pháp:

Sử dụng: Phương trình mặt phẳng \(\left( {Oxz} \right)\) là \(y = 0\)

Hướng dẫn giải:

Phương trình mặt phẳng \(\left( {Oxz} \right)\) là \(y = 0\)

Đáp án D

Câu 15:

Phương pháp:

Hình chiếu vuông góc của \(M\left( {x;y;z} \right)\) lên mặt phẳng \(\left( {Oxz} \right)\) là \(H\left( {x;0;z} \right)\)

Hướng dẫn giải:

Hình chiếu vuông góc của \(A\left( {2; - 4;3} \right)\) lên mặt phẳng \(\left( {Oxz} \right)\) là \(P\left( {2;0;3} \right).\)

Đáp án A

Câu 16:

Phương pháp:

Sử dụng phương pháp đổi biến số để tính tích phân

Hướng dẫn giải:

Đặt \(u = \sqrt {{x^2} + 1} \) \( \Rightarrow du = \frac{x}{{\sqrt {{x^2} + 1} }}dx\)\( \Rightarrow dx = \frac{{\sqrt {{x^2} + 1} }}{x}du = \frac{u}{x}du\)

Đổi cận: Với \(x = 0\) \( \Rightarrow u = \sqrt {{0^2} + 1}  = 1\)

Với \(x = 2\sqrt 2 \) \( \Rightarrow u = \sqrt {{{\left( {2\sqrt 2 } \right)}^2} + 1}  = 3\)

Ta có: \(I = \int\limits_1^{2\sqrt 2 } {2x\sqrt {{x^2} + 1} \,} {\rm{d}}x\)\( = \int\limits_1^3 {2x.u.\frac{u}{x}du} \) \( = \int\limits_1^3 {2{u^2}du}  = \left. {\frac{2}{3}{u^3}} \right|_1^3\)\( = \frac{{52}}{3}\)

Nên A, B, D đúng, C sai.

Đáp án C

Câu 17:

Phương pháp:

Số phức \(z = a + bi\) có phần thực là \(a\) và phần ảo là \(b\) 

Hướng dẫn giải:

Số phức \(z = 1 - 3i\) có phần thực là \(1\) và phần ảo là \( - 3.\)

Đáp án A

Câu 18:

Phương pháp:

Số phức \(z = a + bi\) có số phức liên hợp là \(\overline z  = a - bi\) và có môđun \(\left| z \right| = \sqrt {{a^2} + {b^2}} \) 

Hướng dẫn giải:

Gọi số phức \(z = a + bi\) thì số phức liên hợp của \(z\)  là \(\overline z  = a - bi\) và môđun \(\left| z \right| = \sqrt {{a^2} + {b^2}} \) 

Ta có: \(z.\overline z  = \left( {a + bi} \right)\left( {a - bi} \right)\) \( = {a^2} - {b^2}{i^2} = {a^2} + {b^2} = {\left| z \right|^2}\)

Nên \(z.\bar z = {\left| z \right|^2}.\)

Đáp án A

Câu 19:

Phương pháp:

Sử dụng: \(\int {\frac{1}{{ax + b}}dx}  = \frac{1}{a}\ln \left| {ax + b} \right| + C\)

Hướng dẫn giải:

Ta có \(\int\limits_1^3 {\frac{{{\rm{d}}x}}{{3x + 1}}} \)\( = \left. {\frac{1}{3}\ln \left| {3x + 1} \right|} \right|_1^3\) \( = \frac{1}{3}\left( {\ln 10 - \ln 4} \right)\)\( = \frac{1}{3}\ln \frac{{10}}{4} = \frac{1}{3}\ln \frac{5}{2}\)

Đáp án C

Câu 20:

Phương pháp:

Sử dụng: \(\int {{e^x}dx}  = {e^x} + C\)

Hướng dẫn giải:

Ta có \(\int\limits_0^3 {({e^x}{\rm{ + 1)d}}x}  = \left. {\left( {{e^x} + x} \right)} \right|_0^3\) \( = {e^3} + 3 - \left( {{e^0} + 0} \right)\)\( = {e^3} + 2\)

Đáp án D

Câu 21:

Phương pháp:

Diện tích \(S\) của hình phẳng giới hạn bởi đồ thị hàm số \(y = f\left( x \right)\), trục hoành và hai đường thẳng \(x = a\), \(x = b\) được tính theo công thức \(S = \int\limits_a^b {\left| {f\left( x \right)} \right|\,{\rm{d}}x} .\)

Hướng dẫn giải:

Diện tích \(S\) của hình phẳng giới hạn bởi đồ thị hàm số \(y = f\left( x \right)\), trục hoành và hai đường thẳng \(x = a\), \(x = b\) được tính theo công thức \(S = \int\limits_a^b {\left| {f\left( x \right)} \right|\,{\rm{d}}x} .\)

Đáp án C

Câu 22:

Phương pháp:

Sử dụng: \(\overrightarrow {AB}  = \left( {{x_B} - {x_A};{y_B} - {y_A}} \right)\) với \(A\left( {{x_A};{y_A}} \right),B\left( {{x_B};{y_B}} \right)\)

Hướng dẫn giải:

Ta có \(\overrightarrow {AB}  = \left( {2 - 1; - 2 - 1;1 - \left( { - 2} \right)} \right)\) \( = \left( {1; - 3;3} \right)\)

Đáp án D

Câu 23:

Phương pháp:

Hình phẳng \(\left( H \right)\) giới hạn bởi \(y = f\left( x \right),\) trục hoành và \(x = a;x = b\). Khối tròn xoay tạo thành khi quay \(\left( H \right)\) quanh trục \(Ox\) có thể tích là \(V = \pi \int\limits_a^b {{{\left[ {f\left( x \right)} \right]}^2}} dx\)

Hướng dẫn giải:

Thể tích \(V = \pi \int\limits_1^3 {{{\left( {{x^2} + 5} \right)}^2}{\rm{d}}x} \)

Đáp án D

Câu 24:

Phương pháp:

Khoảng cách từ \(M\left( {{x_0};{y_0};{z_0}} \right)\) đến mặt phẳng \(\left( P \right):ax + by + cz + d = 0\) là: \(d\left( {M;\left( P \right)} \right) = \frac{{\left| {a{x_0} + b{y_0} + c{z_0} + d} \right|}}{{\sqrt {{a^2} + {b^2} + {c^2}} }}\)

Hướng dẫn giải:

Ta có \(d\left( {A;\left( P \right)} \right) = \frac{{\left| {1 + 4\left( { - 2} \right) - 2.3 - 6} \right|}}{{\sqrt {{1^2} + {4^2} + {2^2}} }}\) \( = \frac{{19\sqrt {21} }}{{21}}\)

Đáp án B

Câu 25:

Phương pháp:

Sử dụng: Đường thẳng \(\frac{{x - {x_0}}}{a} = \frac{{y - {y_0}}}{b} = \frac{{z - {z_0}}}{c}\)  có 1 VTCP là \(\overrightarrow u  = \left( {a;b;c} \right)\)

Hướng dẫn giải:

Đường thẳng \(d:\frac{{x + 7}}{2} = \frac{{y - 8}}{{ - 2}} = \frac{{z - 9}}{{ - 3}}\) có một vectơ chỉ phương là  \(\overrightarrow {{u_2}}  = \left( {2; - 2; - 3} \right).\)

Đáp án D

Câu 26:

Phương pháp:

Diện tích \(S\) của hình phẳng giới hạn bởi đồ thị hàm số \(y = f\left( x \right)\), trục hoành và hai đường thẳng \(x = a\), \(x = b\) được tính theo công thức \(S = \int\limits_a^b {\left| {f\left( x \right)} \right|\,{\rm{d}}x} .\)

Hướng dẫn giải:

Ta có \(S = \int\limits_0^2 {\left| {{7^x}} \right|{\rm{d}}x} \)\( = \int\limits_0^2 {{7^x}{\rm{d}}x} \) (vì \({7^x} > 0\) với mọi \(x\))

Đáp án D

Câu 27:

Phương pháp:

Số phức \(z = a + bi\) có số phức liên hợp là \(\overline z  = a - bi\)

Hướng dẫn giải:

Số phức liên hợp của số phức \(z = 3i - 5\) là \(\overline z  =  - 5 - 3i.\)

Đáp án C

Câu 28:

Phương pháp:

Diện tích \(S\) của hình phẳng giới hạn bởi đồ thị hàm số \(y = f\left( x \right)\), \(y = g\left( x \right)\) và hai đường thẳng \(x = a\), \(x = b\) được tính theo công thức \(S = \int\limits_a^b {\left| {f\left( x \right) - g\left( x \right)} \right|\,{\rm{d}}x} .\)

Hướng dẫn giải:

Ta có

 \(\begin{array}{l}S = \int\limits_{ - \frac{1}{3}}^2 {\left| { - {x^2} + 2x + 2 - \left( {2{x^2} - 3x} \right)} \right|dx} \\ = \int\limits_{ - \frac{1}{3}}^2 {\left( { - {x^2} + 2x + 2 - \left( {2{x^2} - 3x} \right)} \right)dx} \\ = \int\limits_{ - \frac{1}{3}}^2 {\left( { - {x^2} + 2x + 2 - 2{x^2} + 3x} \right)dx} \\ = \int\limits_{ - \frac{1}{3}}^2 {\left( { - 3{x^2} + 5x + 2} \right)dx} \end{array}\)

Đáp án A

Câu 29:

Phương pháp:

Số phức \(z = a + bi\) có môđun \(\left| z \right| = \sqrt {{a^2} + {b^2}} \)  

Hướng dẫn giải:

Gọi \(z = x + yi\left( {x;y \in \mathbb{R}} \right)\)

Ta có: \(\left| z \right| = 2 \Leftrightarrow \sqrt {{x^2} + {y^2}}  = 2\) \( \Leftrightarrow {x^2} + {y^2} = 4\)

Vậy tập hợp điểm biểu diễn số phức \(z\) là đường tròn tâm \(O\left( {0;0} \right)\) và bán kính \(R = 2\).

Đáp án D

Câu 30:

Phương pháp:

Sử dụng: \(\left[ {\overrightarrow {AB} ;\overrightarrow {AC} } \right]\) là 1 VTPT của mặt phẳng \(\left( {ABC} \right)\)

Hướng dẫn giải:

Ta có \(\overrightarrow {AB}  = \left( { - 1;1;2} \right),\) \(\overrightarrow {AC}  = \left( { - 3; - 1;0} \right)\)

Mặt phẳng đi qua ba điểm \(A,B,C\) nhận \(\left[ {\overrightarrow {AB} ,\overrightarrow {AC} } \right] = \left( {2; - 6;4} \right)\) làm 1 VTPT

Suy ra  \(\overrightarrow {{n_2}}  = \left( {1; - 3;2} \right)\) cũng là 1 VTPT của \(\left( {ABC} \right)\)

Đáp án D

Câu 31:

Phương pháp:

Sử dụng công thức

\(\begin{array}{l}\overrightarrow u  \pm \overrightarrow v  = \left( {{x_1} \pm {x_2};{y_1} \pm {y_2};{z_1} \pm {z_2}} \right)\\k\overrightarrow u  = \left( {k{x_1};k{y_1};k{z_1}} \right)\end{array}\)

Hướng dẫn giải:

Ta có:

\(\begin{array}{l}\overrightarrow d  = 3\overrightarrow a  - \overrightarrow b  - 2\overrightarrow c \\ = 3\left( { - 2; - 5;0} \right) - \left( {1;2;1} \right) - 2\left( {2;3;2} \right)\\ = \left( { - 6; - 15;0} \right) - \left( {1;2;1} \right) - \left( {4;6;4} \right)\\ = \left( { - 11; - 23; - 5} \right)\end{array}\)

Đáp án D

Câu 32:

Phương pháp:

Đặt \(z = a + bi\left( {a,b \in \mathbb{R}} \right)\), thay vào đẳng thức bài cho tìm \(a,b\).

Hướng dẫn giải:

Đặt \(z = a + bi\left( {a,b \in \mathbb{R}} \right)\) \( \Rightarrow \overline z  = a - bi\) ta có:

\(\begin{array}{l}\left( {1 + 3i} \right)z + 5\overline z  = 4 - i\\ \Leftrightarrow \left( {1 + 3i} \right)\left( {a + bi} \right) + 5\left( {a - bi} \right) = 4 - i\\ \Leftrightarrow a + 3ai + bi + 3b{i^2} + 5a - 5bi = 4 - i\\ \Leftrightarrow \left( {6a - 3b} \right) + \left( {3a - 4b} \right)i = 4 - i\\ \Leftrightarrow \left\{ \begin{array}{l}6a - 3b = 4\\3a - 4b =  - 1\end{array} \right.\\ \Leftrightarrow \left\{ \begin{array}{l}a = \frac{{19}}{{15}}\\b = \frac{6}{5}\end{array} \right.\\ \Rightarrow P = a + b = \frac{{19}}{{15}} + \frac{6}{5} = \frac{{37}}{{15}}\end{array}\)

Đáp án D

Câu 33:

Phương pháp:

Mặt cầu tâm I đi qua A nên nhận \(R = IA\) là bán kính.

Mặt cầu tâm \(I\left( {a;b;c} \right)\) bán kính \(R\) có phương trình:

\({\left( {x - a} \right)^2} + {\left( {y - b} \right)^2} + {\left( {z - c} \right)^2} = {R^2}\)

Hướng dẫn giải:

\(IA = \sqrt {{{\left( { - 1 - 2} \right)}^2} + {{\left( {3 - 1} \right)}^2} + {{\left( {0 - 3} \right)}^2}} \) \( = \sqrt {22} \)

Mặt cầu tâm \(I\left( {2;1;3} \right)\) và đi qua A nên có bán kính \(R = IA = \sqrt {22} \) có phương trình:

\({\left( {x - 2} \right)^2} + {\left( {y - 1} \right)^2} + {\left( {z - 3} \right)^2} = 22.\)

Đáp án D

Câu 34:

Phương pháp:

Phương trình mặt phẳng đi qua điểm \(M\left( {{x_0};{y_0};{z_0}} \right)\) và nhận \(\overrightarrow n  = \left( {a;b;c} \right)\) làm VTPT có phương trình: \(a\left( {x - {x_0}} \right) + b\left( {y - {y_0}} \right) + c\left( {z - {z_0}} \right) = 0\)

Hướng dẫn giải:

Tam giác IKH có M là trực tâm nên \(OM \bot \left( {IKH} \right)\).

Mặt phẳng \(\left( {IKH} \right)\) đi qua \(M\left( {1;2;1} \right)\) và nhận \(\overrightarrow {OM}  = \left( {1;2;1} \right)\) làm VTPT nên có phương trình:

\(\begin{array}{l}1\left( {x - 1} \right) + 2\left( {y - 2} \right) + 1\left( {z - 1} \right) = 0\\ \Leftrightarrow x + 2y + z - 6 = 0\end{array}\)

Đáp án C

Câu 35:

Phương pháp:

Từ tích phân đã cho đặt \(t = ex\) tìm tích phân \(\int\limits_0^e {f\left( x \right)dx} \).

Từ đó suy ra tích phân cần tính giá trị.

Hướng dẫn giải:

Trong tích phân \(\int\limits_0^1 {f\left( {ex} \right){\rm{d}}x}  = 1\), đặt \(t = ex\) ta có:

\(dt = edx \Rightarrow dx = \frac{{dt}}{e}\)

\(x = 0 \Rightarrow t = 0\); \(x = 1 \Rightarrow t = e\)

Khi đó,

\(\begin{array}{l}\int\limits_0^1 {f\left( {ex} \right){\rm{d}}x}  = 1 \Leftrightarrow \int\limits_0^e {f\left( t \right).\frac{{dt}}{e}}  = 1\\ \Leftrightarrow \frac{1}{e}\int\limits_0^e {f\left( t \right)dt}  = 1\\ \Rightarrow \int\limits_0^e {f\left( t \right)dt}  = e \Rightarrow \int\limits_0^e {f\left( x \right)dx}  = e\end{array}\)

\(\begin{array}{l} \Rightarrow \int\limits_0^e {\left[ {f\left( x \right) - e} \right]{\rm{d}}x}  = \int\limits_0^e {f\left( x \right){\rm{d}}x}  - \int\limits_0^e {{\rm{ed}}x} \\ = e - \left. {ex} \right|_0^e = e - {e^2}\end{array}\)

Đáp án D

Câu 36:

Phương pháp:

Sử dụng phương pháp từng phần, đặt \(\left\{ \begin{array}{l}u = x\\dv = f'\left( x \right)dx\end{array} \right.\)

Hướng dẫn giải:

Đặt \(\left\{ \begin{array}{l}u = x\\dv = f'\left( x \right)dx\end{array} \right. \Rightarrow \left\{ \begin{array}{l}du = dx\\v = f\left( x \right)\end{array} \right.\)

\(\begin{array}{l} \Rightarrow \int\limits_0^1 {xf'\left( x \right){\rm{d}}x}  = \left. {xf\left( x \right)} \right|_0^1 - \int\limits_0^1 {f\left( x \right){\rm{d}}x} \\ = 1.f\left( 1 \right) - 0.f\left( 0 \right) - \int\limits_0^1 {f\left( x \right){\rm{d}}x} \\ = 3 - \int\limits_0^1 {f\left( x \right){\rm{d}}x} \\ \Rightarrow m = 3 - \int\limits_0^1 {f\left( x \right){\rm{d}}x} \\ \Rightarrow \int\limits_0^1 {f\left( x \right){\rm{d}}x}  = 3 - m\end{array}\)

Đáp án C

Câu 37:

Phương pháp:

Gọi tọa độ giao điểm của \(\Delta \) với Oy là \(\left( {0;m;0} \right)\).

Sử dụng điều kiện \(\Delta  \bot d\) tìm \(m\). Từ đó viết phương trình \(\Delta \).

Hướng dẫn giải:

Gọi \(M\left( {0;m;0} \right)\) là giao điểm của \(\Delta \) và \(Oy\).

Khi đó \(\Delta \) đi qua \(A,M\) nên nhận \(\overrightarrow {AM}  = \left( { - 2;m - 1; - 3} \right)\) làm VTCP.

\(d:\frac{{x + 1}}{1} = \frac{{y - 1}}{{ - 2}} = \frac{{z - 2}}{2}\) có VTCP \(\overrightarrow {{u_d}}  = \left( {1; - 2;2} \right)\).

\(\begin{array}{l}\Delta  \bot d \Rightarrow \overrightarrow {AM} .\overrightarrow {{u_d}}  = 0\\ \Leftrightarrow  - 2.1 + \left( {m - 1} \right).\left( { - 2} \right) - 3.2 = 0\\ \Leftrightarrow  - 2 - 2m + 2 - 6 = 0\\ \Leftrightarrow  - 2m - 6 = 0\\ \Leftrightarrow m =  - 3\\ \Rightarrow M\left( {0; - 3;0} \right)\\ \Rightarrow \overrightarrow {AM}  = \left( { - 2; - 4; - 3} \right)\end{array}\)

Đường thẳng \(\Delta \) đi qua điểm \(M\left( {0; - 3;0} \right)\) và nhận \( - \overrightarrow {AM}  = \left( {2;4;3} \right)\) làm VTCP nên có phương trình: \(\frac{x}{2} = \frac{{y + 3}}{4} = \frac{z}{3} \cdot \)

Đáp án A

Câu 38:

Phương pháp:

Sử dụng hai số phức bằng nhau \(z = z' \Leftrightarrow \left\{ \begin{array}{l}a = a'\\b = b'\end{array} \right.\).

Hướng dẫn giải:

Ta có:

\(\begin{array}{l}\left( {x + y} \right) + \left( {2x - y} \right)i = 3 - 6i\\ \Leftrightarrow \left\{ \begin{array}{l}x + y = 3\\2x - y =  - 6\end{array} \right.\\ \Leftrightarrow \left\{ \begin{array}{l}x =  - 1\\y = 4\end{array} \right.\end{array}\)

Đáp án D

Câu 39:

Phương pháp:

Tính số phức \(z\), từ đó suy ra \(\overline z \).

Hướng dẫn giải:

Ta có:

\(\begin{array}{l}z = 3i\left( {i - 4} \right) = 3{i^2} - 12i\\ =  - 3 - 12i\\ \Rightarrow \overline z  =  - 3 + 12i\end{array}\)

Đáp án D

Câu 40:

Phương pháp:

Sử dụng công thức Newton – Leibnitz:

Cho \(F\left( x \right)\) là nguyên hàm của hàm số \(f\left( x \right)\). Khi đó,

\(\int\limits_a^b {f\left( x \right)dx}  = F\left( b \right) - F\left( a \right)\)

Hướng dẫn giải:

Ta thấy, \(f\left( x \right)\) là một nguyên hàm của \(f'\left( x \right)\) nên:

\(\begin{array}{l}\int\limits_1^4 {f'(x){\rm{d}}x}  = f\left( 4 \right) - f\left( 1 \right)\\ \Rightarrow 19 = 15 - f\left( 1 \right)\\ \Rightarrow f\left( 1 \right) =  - 4\end{array}\)

Đáp án A

Câu 41:

Phương pháp:

Xét phương trình hoành độ giao điểm của đồ thị hàm số \(y = \ln x\) với trục hoành.

Sử dụng công thức tính diện tích hình phẳng giới hạn bởi đồ thị hàm số \(y = f\left( x \right)\), trục hoành, đường thẳng \(x = a,x = b\) là: \(S = \int\limits_a^b {\left| {f\left( x \right)} \right|dx} \)

Hướng dẫn giải:

Phương trình hoành độ giao điểm: \(\ln x = 0 \Leftrightarrow x = 1\).

Diện tích cần tính: \(S = \int\limits_1^e {\left| {\ln x} \right|dx} \)

Với \(1 \le x \le e\) thì \(\ln x \ge 0\) nên \(\left| {\ln x} \right| = \ln x\). Do đó,

\(S = \int\limits_1^e {\ln xdx} \)

Đặt \(\left\{ \begin{array}{l}u = \ln x\\dv = dx\end{array} \right. \Rightarrow \left\{ \begin{array}{l}du = \frac{1}{x}dx\\v = x\end{array} \right.\)

\(\begin{array}{l} \Rightarrow S = \left. {x\ln x} \right|_1^e - \int\limits_1^e {dx} \\ = e\ln e - 1.\ln 1 - \left. x \right|_1^e\\ = e - \left( {e - 1} \right)\\ = e - e + 1 = 1\end{array}\)

Đáp án D

Câu 42:

Phương pháp:

Thể tích khối tròn xoay do hình phẳng giới hạn bởi các đường \(y = f\left( x \right),\) \(y = 0,\) \(x = a,\) \(x = b\) quay quanh trục \(Ox\) là \(V = \pi \int\limits_a^b {{f^2}\left( x \right)dx} \)

Hướng dẫn giải:

Thể tích khối tròn xoay do hình phẳng giới hạn bởi các đường \(y = \frac{{{x^2} + x + 1}}{{x + 1}},\) \(y = 0,\) \(x = 0,\) \(x = 1\) quay quanh trục \(Ox\) là:

\(\begin{array}{l}V = \pi \int\limits_0^1 {{{\left( {\frac{{{x^2} + x + 1}}{{x + 1}}} \right)}^2}dx} \\ = \pi \int\limits_0^1 {{{\left( {x + \frac{1}{{x + 1}}} \right)}^2}dx} \\ = \pi \int\limits_0^1 {\left( {{x^2} + \frac{{2x}}{{x + 1}} + \frac{1}{{{{\left( {x + 1} \right)}^2}}}} \right)dx} \\ = \pi \left[ {\int\limits_0^1 {{x^2}dx}  + \int\limits_0^1 {\frac{{2x}}{{x + 1}}dx}  + \int\limits_0^1 {\frac{1}{{{{\left( {x + 1} \right)}^2}}}dx} } \right]\\ = \pi \left( {I + J + K} \right)\end{array}\)

ở đó

\(\begin{array}{l}I = \int\limits_0^1 {{x^2}dx}  = \left. {\frac{{{x^3}}}{3}} \right|_0^1 = \frac{1}{3}\\J = \int\limits_0^1 {\frac{{2x}}{{x + 1}}dx}  = 2\int\limits_0^1 {\frac{x}{{x + 1}}dx} \\ = 2\int\limits_0^1 {\left( {1 - \frac{1}{{x + 1}}} \right)dx} \\ = 2\left. {\left( {x - \ln \left| {x + 1} \right|} \right)} \right|_0^1\\ = 2\left( {1 - \ln 2} \right) = 2 - 2\ln 2\\K = \int\limits_0^1 {\frac{1}{{{{\left( {x + 1} \right)}^2}}}dx} \\ = \left. { - \frac{1}{{x + 1}}} \right|_0^1 =  - \left( {\frac{1}{2} - 1} \right) = \frac{1}{2}\\ \Rightarrow S = \pi \left( {I + J + K} \right)\\ = \pi \left( {\frac{1}{3} + 2 - 2\ln 2 + \frac{1}{2}} \right)\\ = \pi \left( {\frac{{17}}{6} - 2\ln 2} \right)\end{array}\)

Đáp án B

Câu 43:

Phương pháp:

Đặt \(z = a + bi\left( {a,b \in \mathbb{R}} \right)\), thay vào đẳng thức đã cho tìm mối quan hệ của \(a,b\).

Thay vào công thức tính \(\left| z \right|\) và tìm GTNN.

Hướng dẫn giải:

Đặt \(z = a + bi\left( {a,b \in \mathbb{R}} \right)\) ta có:

\(\begin{array}{l}\left| {z - 1 + 3i} \right| = \left| {z - 2i} \right|\\ \Leftrightarrow \left| {a + bi - 1 + 3i} \right| = \left| {a + bi - 2i} \right|\\ \Leftrightarrow \left| {\left( {a - 1} \right) + \left( {b + 3} \right)i} \right| = \left| {a + \left( {b - 2} \right)i} \right|\\ \Leftrightarrow \sqrt {{{\left( {a - 1} \right)}^2} + {{\left( {b + 3} \right)}^2}}  = \sqrt {{a^2} + {{\left( {b - 2} \right)}^2}} \\ \Leftrightarrow {\left( {a - 1} \right)^2} + {\left( {b + 3} \right)^2} = {a^2} + {\left( {b - 2} \right)^2}\\ \Leftrightarrow {a^2} - 2a + 1 + {b^2} + 6b + 9\\ = {a^2} + {b^2} - 4b + 4\\ \Leftrightarrow  - 2a + 6b + 10 =  - 4b + 4\\ \Leftrightarrow  - 2a + 10b + 6 = 0\\ \Leftrightarrow a - 5b - 3 = 0\\ \Leftrightarrow a = 5b + 3\\ \Rightarrow \left| z \right| = \sqrt {{a^2} + {b^2}} \\ = \sqrt {{{\left( {5b + 3} \right)}^2} + {b^2}} \\ = \sqrt {25{b^2} + 30b + 9 + {b^2}} \\ = \sqrt {26{b^2} + 30b + 9} \\ = \sqrt {26\left( {{b^2} + \frac{{15}}{{13}}b + \frac{{225}}{{676}}} \right) + \frac{9}{{26}}} \\ = \sqrt {26{{\left( {b + \frac{{15}}{{26}}} \right)}^2} + \frac{9}{{26}}} \\ \ge \sqrt {26.0 + \frac{9}{{26}}}  = \frac{{3\sqrt {26} }}{{26}}\end{array}\)

\( \Rightarrow {\left| z \right|_{\min }} = \frac{{3\sqrt {26} }}{{26}}\) khi \(b =  - \frac{{15}}{{26}} \Rightarrow a = \frac{3}{{26}}\) \( \Rightarrow z = \frac{3}{{26}} - \frac{{15}}{{26}}i\)

Đáp án A

Câu 44:

Phương pháp:

- Viết phương trình các đường thẳng \(AB,OC\).

- Gọi tọa độ các điểm \(M,N\) theo tham số hóa.

- Thay vào điều kiện \(AM = ON\) tìm mối quan hệ giữa hai tham số trên.

- Từ đó tìm GTNN của \(MN\).

Hướng dẫn giải:

Ta có: \(\overrightarrow {AB}  = \left( { - 6;0;6} \right)\), \(\overrightarrow {OC}  = \left( {0;6;6} \right)\).

Đường thẳng AB đi qua \(A\left( {6;0;0} \right)\) và nhận \(\frac{1}{6}\overrightarrow {AB}  = \left( { - 1;0;1} \right)\) làm VTCP nên \(AB:\left\{ \begin{array}{l}x = 6 - t\\y = 0\\z = t\end{array} \right.\)

\(M \in AB \Rightarrow M\left( {6 - t;0;t} \right)\) (\(0 < t < 6\) do \(M\) thuộc đoạn \(AB\))

\( \Rightarrow AM = \sqrt {{{\left( { - t} \right)}^2} + 0 + {t^2}}  = \sqrt {2{t^2}} \)

Đường thẳng \(OC\) đi qua \(O\left( {0;0;0} \right)\) và nhận \(\frac{1}{6}\overrightarrow {OC}  = \left( {0;1;1} \right)\) làm VTCP nên \(OC:\left\{ \begin{array}{l}x = 0\\y = t'\\y = t'\end{array} \right.\)

\(N \in OC \Rightarrow N\left( {0;t';t'} \right)\) (\(0 < t' < 6\) do \(N\) thuộc đoạn \(OC\))

\( \Rightarrow ON = \sqrt {0 + t{'^2} + t{'^2}}  = \sqrt {2t{'^2}} \)

Theo giả thiết

\(\begin{array}{l}AM = ON\\ \Rightarrow \sqrt {2{t^2}}  = \sqrt {2t{'^2}}  \Leftrightarrow 2{t^2} = 2t{'^2}\\ \Leftrightarrow {t^2} = t{'^2}\\ \Leftrightarrow \left[ \begin{array}{l}t = t'\,\,\left( {TM} \right)\\t =  - t'\,\left( {loai\,do\,t,t' > 0} \right)\end{array} \right.\end{array}\)

\(\begin{array}{l} \Rightarrow M\left( {6 - t;0;t} \right),N\left( {0;t;t} \right)\\ \Rightarrow MN = \sqrt {{{\left( {t - 6} \right)}^2} + {t^2} + 0} \\ = \sqrt {2{t^2} - 12t + 36} \\ = \sqrt {2\left( {{t^2} - 6t + 9} \right) + 18} \\ = \sqrt {2{{\left( {t - 3} \right)}^2} + 18} \\ \ge \sqrt {2.0 + 18}  = 3\sqrt 2 \\ \Rightarrow MN \ge 3\sqrt 2 \end{array}\)

Dấu “=” xảy ra khi \(t = 3\) \( \Rightarrow M\left( {3;0;3} \right),N\left( {0;3;3} \right)\)

\( \Rightarrow \overrightarrow {MN}  = \left( { - 3;3;0} \right)\)

Đường thẳng \(MN\) đi qua điểm \(M\left( {3;0;3} \right)\) và nhận \( - \frac{1}{3}\overrightarrow {MN}  = \left( {1; - 1;0} \right)\) làm VTCP nên có phương trình: \(\left\{ \begin{array}{l}x = 3 + t\\y =  - t\\z = 3\end{array} \right.,t \in \mathbb{R}\)

Đáp án C

Câu 45:

Phương pháp:

Gắn hệ trục tọa độ, viết phương trình parabol và suy ra diện tích theo công thức:

\(S = \int\limits_a^b {\left| {f\left( x \right)} \right|dx} \)

Hướng dẫn giải:

Gắn hệ trục tọa độ như hình vẽ.

Gọi phương trình parabol là \(y = a{x^2} + bx + c\) (P)

\(C\left( {0;7} \right)\) là đỉnh nên \( - \frac{b}{{2a}} = 0 \Rightarrow b = 0\)\( \Rightarrow y = a{x^2} + c\).

\(\left( P \right)\) đi qua \(C\left( {0;7} \right)\) nên \(7 = a{.0^2} + c \Rightarrow c = 7\)

\( \Rightarrow y = a{x^2} + 7\)

\(B\left( {4;0} \right)\) thuộc \(\left( P \right)\) nên \(0 = a{.4^2} + 7 \Rightarrow a =  - \frac{7}{{16}}\)

\( \Rightarrow \left( P \right):y =  - \frac{7}{{16}}{x^2} + 7\)

Diện tích cần tìm:

\(\begin{array}{l}S = \int\limits_{ - 4}^4 {\left( { - \frac{7}{{16}}{x^2} + 7} \right)dx} \\ = \left. {\left( { - \frac{7}{{16}}.\frac{{{x^3}}}{3} + 7x} \right)} \right|_{ - 4}^4\\ =  - \frac{7}{{16}}\left( {\frac{{{4^3}}}{3} - \frac{{{{\left( { - 4} \right)}^3}}}{3}} \right) + 7\left( {4 + 4} \right)\\ = \frac{{112}}{3}\end{array}\)

Đáp án D

Câu 46:

Phương pháp:

Tìm hàm số \(f\left( x \right)\) từ giả thiết \(f'\left( x \right) = \frac{{ - 2x - 3}}{{{{\left( {{x^2} + 3x + 2} \right)}^2}}}\) và \(f\left( 1 \right) = \frac{1}{6}\).

Thay vào tính tích phân \(\int\limits_0^1 {f\left( x \right)dx} \).

Hướng dẫn giải:

Ta có:

\(\begin{array}{l}f\prime \left( x \right) = \frac{{ - 2x - 3}}{{{{\left( {{x^2} + 3x + 2} \right)}^2}}}\\ \Rightarrow f\left( x \right) = \int {\frac{{ - 2x - 3}}{{{{\left( {{x^2} + 3x + 2} \right)}^2}}}dx} \end{array}\)

Đặt \(t = {x^2} + 3x + 2\) \( \Rightarrow dt = \left( {2x + 3} \right)dx\)

\(\begin{array}{l} \Rightarrow f\left( x \right) = \int {\frac{{ - dt}}{{{t^2}}}}  = \frac{1}{t} + C\\ = \frac{1}{{{x^2} + 3x + 2}} + C\\f\left( 1 \right) = \frac{1}{6} \Rightarrow \frac{1}{{1 + 3 + 2}} + C = \frac{1}{6}\\ \Rightarrow C = 0\\ \Rightarrow f\left( x \right) = \frac{1}{{{x^2} + 3x + 2}}\end{array}\)

\(\begin{array}{l} \Rightarrow \int\limits_0^1 {f\left( x \right)dx}  = \int\limits_0^1 {\frac{1}{{{x^2} + 3x + 2}}dx} \\ = \int\limits_0^1 {\frac{1}{{\left( {x + 1} \right)\left( {x + 2} \right)}}dx} \\ = \int\limits_0^1 {\frac{{\left( {x + 2} \right) - \left( {x + 1} \right)}}{{\left( {x + 1} \right)\left( {x + 2} \right)}}dx} \\ = \int\limits_0^1 {\left[ {\frac{{x + 2}}{{\left( {x + 1} \right)\left( {x + 2} \right)}} - \frac{{x + 1}}{{\left( {x + 1} \right)\left( {x + 2} \right)}}} \right]dx} \\ = \int\limits_0^1 {\left( {\frac{1}{{x + 1}} - \frac{1}{{x + 2}}} \right)dx} \\ = \left. {\left( {\ln \left| {x + 1} \right| - \ln \left| {x + 2} \right|} \right)} \right|_0^1\\ = \left. {\left( {\ln \left| {\frac{{x + 1}}{{x + 2}}} \right|} \right)} \right|_0^1\\ = \ln \frac{2}{3} - \ln \frac{1}{2} = \ln \frac{4}{3}\end{array}\)

Đáp án C

Câu 47:

Phương pháp:

Đặt \(t = \sqrt {1 + {{\sin }^2}x} \) tính tích phân đã cho.

Hướng dẫn giải:

Đặt \(t = \sqrt {1 + {{\sin }^2}x} \)

\( \Rightarrow {t^2} = 1 + {\sin ^2}x\) \( \Rightarrow 2tdt = 2\sin x\cos xdx = \sin 2xdx\)

Đổi cận: \(x = 0 \Rightarrow t = 1;\) \(x = m \Rightarrow t = \sqrt {1 + {{\sin }^2}m} \)

\(\begin{array}{l} \Rightarrow \int\limits_0^m {\sin 2x\sqrt {1 + {{\sin }^2}x} {\rm{d}}x = 0} \\ \Leftrightarrow \int\limits_1^{\sqrt {1 + {{\sin }^2}m} } {2{t^2}dt}  = 0\\ \Leftrightarrow \left. {\frac{{2{t^3}}}{3}} \right|_1^{\sqrt {1 + {{\sin }^2}m} } = 0\\ \Leftrightarrow \frac{2}{3}{\left( {\sqrt {1 + {{\sin }^2}m} } \right)^3} - \frac{2}{3} = 0\\ \Leftrightarrow {\left( {\sqrt {1 + {{\sin }^2}m} } \right)^3} = 1\\ \Leftrightarrow \sqrt {1 + {{\sin }^2}m}  = 1\\ \Leftrightarrow {\sin ^2}m = 0 \Leftrightarrow \sin m = 0\\ \Leftrightarrow m = k\pi \end{array}\)

Mà

\(\begin{array}{l}0 < m \le 2020\\ \Rightarrow 0 < k\pi  \le 2020\\ \Rightarrow 0 < k \le \frac{{2020}}{\pi }\\k \in \mathbb{Z} \Rightarrow k \in \left\{ {1;2;...;642} \right\}\end{array}\)

Vậy có tất cả \(642\) giá trị của \(m\) thỏa mãn bài toán.

Đáp án C

Câu 48:

Phương pháp:

Gọi tọa độ điểm \(B\left( {0;b;0} \right),C\left( {0;0;c} \right)\) lần lượt thuộc \(Oy,Oz\).

Lập hệ phương trình ẩn \(b,c\) vừa gọi.

Giải hệ tìm \(b,c\) và kết luận.

Hướng dẫn giải:

Gọi tọa độ điểm \(B\left( {0;b;0} \right),C\left( {0;0;c} \right)\) lần lượt thuộc tia \(Oy,Oz\) (\(b,c > 0\))

Phương trình \(\left( {ABC} \right)\) là: \(\frac{x}{2} + \frac{y}{b} + \frac{z}{c} = 1\)\( \Rightarrow \overrightarrow n  = \left( {\frac{1}{2};\frac{1}{b};\frac{1}{c}} \right)\) là VTPT của \(\left( {ABC} \right)\).

\(\left( P \right):3y - 3z + 7 = 0\) \( \Rightarrow \overrightarrow {{n_P}}  = \left( {0;3; - 3} \right)\) là VTPT của \(\left( P \right)\).

\(\begin{array}{l}\left( {ABC} \right) \bot \left( P \right) \Leftrightarrow \overrightarrow n .\overrightarrow {{n_P}}  = 0\\ \Leftrightarrow \frac{1}{2}.0 + \frac{1}{b}.3 + \frac{1}{c}.\left( { - 3} \right) = 0\\ \Leftrightarrow \frac{3}{b} - \frac{3}{c} = 0 \Leftrightarrow b = c\end{array}\)

\( \Rightarrow \left( {ABC} \right):\frac{x}{2} + \frac{y}{b} + \frac{z}{b} - 1 = 0\)

\(\begin{array}{l}d\left( {O,\left( {ABC} \right)} \right) = \sqrt 2 \\ \Leftrightarrow \frac{{\left| { - 1} \right|}}{{\sqrt {{{\left( {\frac{1}{2}} \right)}^2} + {{\left( {\frac{1}{b}} \right)}^2} + {{\left( {\frac{1}{b}} \right)}^2}} }} = \sqrt 2 \\ \Leftrightarrow \sqrt {{{\left( {\frac{1}{2}} \right)}^2} + {{\left( {\frac{1}{b}} \right)}^2} + {{\left( {\frac{1}{b}} \right)}^2}}  = \frac{1}{{\sqrt 2 }}\\ \Leftrightarrow {\left( {\frac{1}{2}} \right)^2} + {\left( {\frac{1}{b}} \right)^2} + {\left( {\frac{1}{b}} \right)^2} = \frac{1}{2}\\ \Leftrightarrow \frac{1}{4} + \frac{2}{{{b^2}}} = \frac{1}{2} \Leftrightarrow \frac{2}{{{b^2}}} = \frac{1}{4}\\ \Leftrightarrow {b^2} = 8 \Leftrightarrow b = 2\sqrt 2 \left( {do\,b > 0} \right)\\ \Rightarrow B\left( {0;2\sqrt 2 ;0} \right),C\left( {0;0;2\sqrt 2 } \right)\end{array}\)

Đáp án A

Câu 49:

Phương pháp:

Chứng minh và sử dụng đẳng thức \({\left| {{z_1} + {z_2}} \right|^2} + {\left| {{z_1} - {z_2}} \right|^2} = 2\left( {{{\left| {{z_1}} \right|}^2} + {{\left| {{z_2}} \right|}^2}} \right)\)

Hướng dẫn giải:

Đặt \({z_1} = {a_1} + {b_1}i,{z_2} = {a_2} + {b_2}i\)

Ta chứng minh đẳng thức: \({\left| {{z_1} + {z_2}} \right|^2} + {\left| {{z_1} - {z_2}} \right|^2}\) \( = 2\left( {{{\left| {{z_1}} \right|}^2} + {{\left| {{z_2}} \right|}^2}} \right)\)  (*)

\(\begin{array}{l} \Rightarrow {z_1} + {z_2} = \left( {{a_1} + {a_2}} \right) + \left( {{b_1} + {b_2}} \right)i\\ \Rightarrow \left| {{z_1} + {z_2}} \right| = \sqrt {{{\left( {{a_1} + {a_2}} \right)}^2} + {{\left( {{b_1} + {b_2}} \right)}^2}} \\ \Rightarrow {\left| {{z_1} + {z_2}} \right|^2} = {\left( {{a_1} + {a_2}} \right)^2} + {\left( {{b_1} + {b_2}} \right)^2}\\{z_1} - {z_2} = \left( {{a_1} - {a_2}} \right) + \left( {{b_1} - {b_2}} \right)i\\ \Rightarrow \left| {{z_1} - {z_2}} \right| = \sqrt {{{\left( {{a_1} - {a_2}} \right)}^2} + {{\left( {{b_1} - {b_2}} \right)}^2}} \\ \Rightarrow {\left| {{z_1} - {z_2}} \right|^2} = {\left( {{a_1} - {a_2}} \right)^2} + {\left( {{b_1} - {b_2}} \right)^2}\\ \Rightarrow {\left| {{z_1} + {z_2}} \right|^2} + {\left| {{z_1} - {z_2}} \right|^2}\\ = {\left( {{a_1} + {a_2}} \right)^2} + {\left( {{b_1} + {b_2}} \right)^2}\\ + {\left( {{a_1} - {a_2}} \right)^2} + {\left( {{b_1} - {b_2}} \right)^2}\\ = a_1^2 + 2{a_1}{a_2} + a_2^2 + b_1^2 + 2{b_1}{b_2} + b_2^2\\ + a_1^2 - 2{a_1}{a_2} + a_2^2 + b_1^2 - 2{b_1}{b_2} + b_2^2\\ = 2\left( {a_1^2 + a_2^2 + b_1^2 + b_2^2} \right)\\{\left| {{z_1}} \right|^2} = {\left( {\sqrt {a_1^2 + b_1^2} } \right)^2} = a_1^2 + b_1^2\\{\left| {{z_2}} \right|^2} = {\left( {\sqrt {a_2^2 + b_2^2} } \right)^2} = a_2^2 + b_2^2\\ \Rightarrow {\left| {{z_1}} \right|^2} + {\left| {{z_2}} \right|^2} = a_1^2 + a_2^2 + b_1^2 + b_2^2\end{array}\)

\( \Rightarrow {\left| {{z_1} + {z_2}} \right|^2} + {\left| {{z_1} - {z_2}} \right|^2}\) \( = 2\left( {{{\left| {{z_1}} \right|}^2} + {{\left| {{z_2}} \right|}^2}} \right)\)

Theo bài ra, \(\left| {{z_1}} \right| = 4,\left| {{z_2}} \right| = 2,\left| {{z_1} - {z_2}} \right| = 3\) nên:

\(\begin{array}{l}{\left| {{z_1} + {z_2}} \right|^2} + {3^2} = 2\left( {{4^2} + {2^2}} \right)\\ \Rightarrow {\left| {{z_1} + {z_2}} \right|^2} = 31\\ \Rightarrow \left| {{z_1} + {z_2}} \right| = \sqrt {31} \end{array}\)

Đáp án D

Câu 50:

Phương pháp:

Gọi tọa độ điểm \(M\left( {0;b;c} \right) \in \left( {Oyz} \right)\).

Thay vào biểu thức \(T\) tìm GTNN, từ đó suy ra \(b,c\) và kết luận.

Hướng dẫn giải:

\(M\left( {a;b;c} \right) \in \left( {Oyz} \right)\) \( \Rightarrow M\left( {0;b;c} \right)\)

\(\begin{array}{l} \Rightarrow AM = \sqrt {1 + {b^2} + {c^2}} \\BM = \sqrt {9 + {{\left( {b - 2} \right)}^2} + {{\left( {c - 4} \right)}^2}} \\CM = \sqrt {{{\left( {b - 5} \right)}^2} + {{\left( {c - 4} \right)}^2}} \\ \Rightarrow A{M^2} = 1 + {b^2} + {c^2}\\B{M^2} = 9 + {\left( {b - 2} \right)^2} + {\left( {c - 4} \right)^2}\\C{M^2} = {\left( {b - 5} \right)^2} + {\left( {c - 4} \right)^2}\\ \Rightarrow T = A{M^2} + B{M^2} + 2C{M^2}\\ = 1 + {b^2} + {c^2}\\ + 9 + {\left( {b - 2} \right)^2} + {\left( {c - 4} \right)^2}\\ + 2\left[ {{{\left( {b - 5} \right)}^2} + {{\left( {c - 4} \right)}^2}} \right]\\ = 1 + {b^2} + {c^2}\\ + 9 + {b^2} - 4b + 4 + {c^2} - 8c + 16\\ + 2\left( {{b^2} - 10b + 25 + {c^2} - 8c + 16} \right)\\ = 112 + 4{b^2} + 4{c^2} - 24b - 24c\\ = 4\left( {{b^2} + {c^2} - 6b - 6c + 28} \right)\\ = 4\left[ {{{\left( {b - 3} \right)}^2} + {{\left( {c - 3} \right)}^2} + 10} \right]\\ \ge 4.\left( {0 + 0 + 10} \right) = 40\\ \Rightarrow T \ge 40\end{array}\)

\( \Rightarrow {T_{\min }} = 40\) khi \(b = c = 3\)

Vậy \(a + b + c = 0 + 3 + 3 = 6\)

Đáp án B

HocTot.Nam.Name.Vn