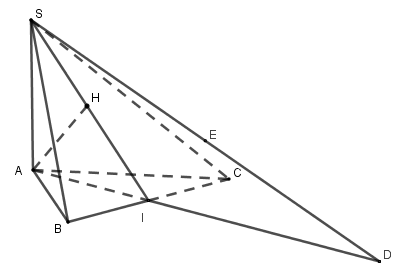
Giải đề thi học kì 2 toán lớp 11 năm 2019 - 2020 trường THPT Bùi Thị Xuân - TP Hồ Chí Minh

PHẦN ĐẠI SỐ (6 điểm)

Bài 1

Tính giới hạn $\mathop {\lim }\limits_{x \to  + \infty } \frac{{x\left( {\sqrt {4{x^2} + x + 1}  + 3x} \right)}}{{{x^2} + 2}}$

Bài 2

Cho hàm số $f\left( x \right) = \left\{ \begin{array}{l}\frac{{{x^3} - 5{x^2} + 12}}{{2x - 4}}\,\,\,\left( {x \ne 2} \right)\\3{a^2} - 7\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\left( {x = 2} \right)\end{array} \right.$

Định $a$ để hàm số liên tục tại điểm $x = 2$.

Bài 3

Tính đạo hàm các hàm số sau:

a) $y = \sqrt {{x^2} + 3x + 1}$

b) $y = \left( {2x - 5} \right)\sin 3x$

Bài 4

Một vật chuyển động có phương trình $S\left( t \right) = \frac{{2{t^3}}}{3} - \frac{1}{t} + 6$, trong đó $t$ (tính bằng giây) là thời gian vật chuyển động kể từ lúc bắt đầu chuyển động $\left( {t > 0} \right)$ và $S$ (tính bằng mét) là quãng đường vật đi được trong khoảng thời gian $t$. Tính vận tốc và gia tốc của vật tại thời điểm $t = 5\left( s \right)$.

Bài 5

Cho hàm số $y = {x^3} + 3{x^2} - 1$ có đồ thị $\left( C \right)$. Viết phương trình tiếp tuyến $\Delta$ của đồ thị $\left( C \right)$, biết tiếp tuyến $\Delta$ song song đường thẳng $d:y = 9x - 6$.

Bài 6

Chứng minh phương trình $\left( {{m^2} + 2m + 6} \right){x^4} + x - 2 = 0$ luôn có nghiệm với mọi giá trị thực của tham số $m$.

PHẦN HÌNH HỌC (4 điểm)

Bài 7

Cho tứ diện $SABC$ có $SA,AB,AC$ đôi một vuông góc, biết $SA = AB = AC = a$. Gọi $I$ là trung điểm của đoạn $BC$.

a) Chứng minh đường thẳng $SA$ vuông góc với mặt phẳng $\left( {ABC} \right)$. Chứng minh mặt phẳng $\left( {SAB} \right)$ vuông góc với mặt phẳng $\left( {SAC} \right)$.

b) Chứng minh mặt phẳng $\left( {SAI} \right)$ vuông góc với mặt phẳng $\left( {SBC} \right)$.

c) Tính góc giữa hai mặt phẳng $\left( {SAB} \right)$ và $\left( {SAI} \right)$.

d) Trên tia đối của tia $IA$ lấy điểm $D$ sao cho $ID = 2IA$ và gọi $E$ là trung điểm của đoạn $SD$. Tính khoảng cách từ điểm $E$ đến mặt phẳng $\left( {SBC} \right)$ theo $a$.

HẾT

HƯỚNG DẪN GIẢI CHI TIẾT

Thực hiện: Ban chuyên môn HocTot.Nam.Name.Vn

Bài 1 (VD):

Phương pháp:

Chia cả tử và mẫu cho ${x^2}$.

Cách giải:

$\begin{array}{l}\mathop {\lim }\limits_{x \to  + \infty } \frac{{x\left( {\sqrt {4{x^2} + x + 1}  + 3x} \right)}}{{{x^2} + 2}}\\ = \mathop {\lim }\limits_{x \to  + \infty } \frac{{x\left( {\sqrt {{x^2}\left( {4 + \frac{1}{x} + \frac{1}{{{x^2}}}} \right)}  + 3x} \right)}}{{{x^2} + 2}}\\ = \mathop {\lim }\limits_{x \to  + \infty } \frac{{x\left( {\left| x \right|\sqrt {4 + \frac{1}{x} + \frac{1}{{{x^2}}}}  + 3x} \right)}}{{{x^2} + 2}}\\ = \mathop {\lim }\limits_{x \to  + \infty } \frac{{x\left( {x\sqrt {4 + \frac{1}{x} + \frac{1}{{{x^2}}}}  + 3x} \right)}}{{{x^2} + 2}}\\ = \mathop {\lim }\limits_{x \to  + \infty } \frac{{{x^2}\left( {\sqrt {4 + \frac{1}{x} + \frac{1}{{{x^2}}}}  + 3} \right)}}{{{x^2}\left( {1 + \frac{2}{{{x^2}}}} \right)}}\\ = \mathop {\lim }\limits_{x \to  + \infty } \frac{{\sqrt {4 + \frac{1}{x} + \frac{1}{{{x^2}}}}  + 3}}{{1 + \frac{2}{{{x^2}}}}}\\ = \frac{{\sqrt {4 + 0 + 0}  + 3}}{{1 + 0}} = 5\end{array}$

Bài 2 (VD):

Phương pháp:

Hàm số $y = f\left( x \right)$ liên tục tại $x = {x_0}$ $\Leftrightarrow \mathop {\lim }\limits_{x \to {x_0}} f\left( x \right) = f\left( {{x_0}} \right)$.

Cách giải:

Ta có:

$\begin{array}{l}\mathop {\lim }\limits_{x \to 2} f\left( x \right) = \mathop {\lim }\limits_{x \to 2} \frac{{{x^3} - 5{x^2} + 12}}{{2x - 4}}\\ = \mathop {\lim }\limits_{x \to 2} \frac{{\left( {x - 2} \right)\left( {{x^2} - 3x - 6} \right)}}{{2\left( {x - 2} \right)}}\\ = \mathop {\lim }\limits_{x \to 2} \frac{{{x^2} - 3x - 6}}{2}\\ = \frac{{{2^2} - 3.2 - 6}}{2} =  - 4\\f\left( 2 \right) = 3{a^2} - 7\end{array}$

Để hàm số liên tục tại $x = 2$ thì:

$\begin{array}{l}\mathop {\lim }\limits_{x \to 2} f\left( x \right) = f\left( 2 \right)\\ \Leftrightarrow  - 4 = 3{a^2} - 7\\ \Leftrightarrow 3{a^2} = 3\\ \Leftrightarrow {a^2} = 1\\ \Leftrightarrow a =  \pm 1\end{array}$

Vậy $a =  \pm 1$.

Bài 3 (VD):

Phương pháp:

Sử dụng các công thức tính đạo hàm:

$\left( {\sqrt u } \right)' = \frac{{u'}}{{2\sqrt u }}$

$\left( {uv} \right)' = u'v + uv'$

$\left( {\sin u} \right)' = u'\cos u$

Cách giải:

a)$y = \sqrt {{x^2} + 3x + 1}$

$\begin{array}{l}y' = \left( {\sqrt {{x^2} + 3x + 1} } \right)'\\ = \frac{{\left( {{x^2} + 3x + 1} \right)'}}{{2\sqrt {{x^2} + 3x + 1} }}\\ = \frac{{2x + 3}}{{2\sqrt {{x^2} + 3x + 1} }}\end{array}$

Vậy $y' = \frac{{2x + 3}}{{2\sqrt {{x^2} + 3x + 1} }}$

b) $y = \left( {2x - 5} \right)\sin 3x$

$\begin{array}{l}y'\\ = \left( {2x - 5} \right)'\sin 3x + \left( {2x - 5} \right)\left( {\sin 3x} \right)'\\ = 2\sin 3x + \left( {2x - 5} \right).\left( {3x} \right)'\cos 3x\\ = 2\sin 3x + 3\left( {2x - 5} \right)\cos 3x\\ = 2\sin 3x + \left( {6x - 15} \right)\cos 30\end{array}$

Vậy $y' = 2\sin 3x + \left( {6x - 15} \right)\cos 3x$

Bài 4 (VD):

Phương pháp:

Sử dụng công thức

$\begin{array}{l}v\left( t \right) = S'\left( t \right)\\a\left( t \right) = v'\left( t \right)\end{array}$

Cách giải:

Ta có:

$\begin{array}{l}S\left( t \right) = \frac{{2{t^3}}}{3} - \frac{1}{t} + 6\\v\left( t \right) = S'\left( t \right) = \left( {\frac{{2{t^3}}}{3} - \frac{1}{t} + 6} \right)'\\ = \frac{{2.3{t^2}}}{3} - \left( { - \frac{1}{{{t^2}}}} \right) + 0\\ = 2{t^2} + \frac{1}{{{t^2}}}\\a\left( t \right) = v'\left( t \right) = \left( {2{t^2} + \frac{1}{{{t^2}}}} \right)'\\ = 2.2t + \frac{{ - 2t}}{{{t^4}}} = 4t - \frac{2}{{{t^3}}}\end{array}$

Với $t = 5$ thì

$\begin{array}{l}v\left( 5 \right) = {2.5^2} + \frac{1}{{{5^2}}} = 50,04\left( {m/s} \right)\\a\left( 5 \right) = 4.5 - \frac{2}{{{5^3}}} = 19,984\left( {m/{s^2}} \right)\end{array}$

Vậy tại thời điểm $t = 5\left( s \right)$ thì vận tốc của vật là $50,04m/s$ và gia tốc của vật là $19,984m/{s^2}$.

Bài 5 (VD):

Phương pháp:

- Tính $y'$.

- Giải phương trình $k = f'\left( {{x_0}} \right) = {k_d}$ với ${k_d}$ là hệ số góc của $d$.

- Từ đó viết phương trình tiếp tuyến theo công thức $y = k\left( {x - {x_0}} \right) + {y_0}$.

Cách giải:

Đặt $y = f\left( x \right) = {x^3} + 3{x^2} - 1$.

Ta có: $f'\left( x \right) = 3{x^2} + 6x$.

Gọi $M\left( {{x_0};{y_0}} \right)$ là tọa độ tiếp điểm.

$\Delta //d:y = 9x - 6$ $\Rightarrow$hệ số góc của $\Delta$ là ${k_\Delta } = {k_d} = 9$

$\begin{array}{l} \Rightarrow f'\left( {{x_0}} \right) = 9\\ \Leftrightarrow 3x_0^2 + 6{x_0} = 9\\ \Leftrightarrow 3x_0^2 + 6{x_0} - 9 = 0\\ \Leftrightarrow \left[ \begin{array}{l}{x_0} = 1\\{x_0} =  - 3\end{array} \right.\end{array}$

+) Với ${x_0} = 1$ thì ${y_0} = {1^3} + {3.1^2} - 1 = 3$.

Phương trình tiếp tuyến tại $M\left( {1;3} \right)$ là: $y = 9\left( {x - 1} \right) + 3$ hay $y = 9x - 6$ (loại vì trùng với $d$)

+) Với ${x_0} =  - 3$ thì ${y_0} = {\left( { - 3} \right)^3} + 3.{\left( { - 3} \right)^2} - 1 =  - 1$.

Phương trình tiếp tuyến tại $M\left( { - 3; - 1} \right)$ là: $y = 9\left( {x + 3} \right) - 1$ hay $y = 9x + 26$ (thỏa mãn)

Vậy tiếp tuyến cần tìm có phương trình: $\Delta :y = 9x + 26$.

Bài 6 (VD):

Phương pháp:

Sử dụng định lý: “Nếu hàm số $y = f\left( x \right)$ liên tục trên $\left[ {a;b} \right]$ và $f\left( a \right).f\left( b \right) < 0$ thì tồn tại ít nhất một điểm $c \in \left( {a;b} \right)$ sao cho $f\left( c \right) = 0$”.

Cách giải:

Đặt $f\left( x \right) = \left( {{m^2} + 2m + 6} \right){x^4} + x - 2$.

TXĐ: $D = \mathbb{R}$.

Hàm số $f\left( x \right)$ là hàm đa thức nên liên tục trên $\mathbb{R}$, do đó cung liên tục trên $\left[ {0;1} \right]$.

Ta có:

$f\left( 0 \right) = \left( {{m^2} + 2m + 6} \right){.0^4} + 0 - 2$ $=  - 2 < 0$

$f\left( 1 \right) = \left( {{m^2} + 2m + 6} \right){.1^4} + 1 - 2$ $= {m^2} + 2m + 5$ $= {m^2} + 2m + 1 + 4$ $= {\left( {m + 1} \right)^2} + 4 > 0,\forall m$

Do đó $f\left( 0 \right).f\left( 1 \right)$ $=  - 2\left( {{m^2} + 2m + 5} \right) < 0,\forall m$.

Vậy phương trình $f\left( x \right) = 0$ có ít nhất một nghiệm thuộc khoảng $\left( {0;1} \right)$ hay phương trình đã cho luôn có nghiệm với mọi $m$.

Bài 7 (VD):

Phương pháp:

a) Chứng minh $SA$ vuông góc với hai đường thẳng cắt nhau nằm trong $\left( {ABC} \right)$

Chứng minh $AB \bot \left( {SAC} \right)$ sau đó sử dụng $\left\{ \begin{array}{l}a \bot \left( P \right)\\b \subset \left( P \right)\end{array} \right.$ $\Rightarrow a \bot b$

b) Chứng minh $BC \bot \left( {SAI} \right)$ sau đó sử dụng $\left\{ \begin{array}{l}a \bot \left( P \right)\\b \subset \left( P \right)\end{array} \right.$ $\Rightarrow a \bot b$

c) Sử dụng $\left\{ \begin{array}{l}\left( P \right) \cap \left( Q \right) = d\\a \bot d;a \subset \left( P \right)\\b \bot d;b \subset \left( Q \right)\end{array} \right.$  thì góc giữa $\left( P \right)$ và $\left( Q \right)$ là góc giữa hai đường thẳng $a$ và $b$

d) Sử dụng: Nếu $AB \cap \left( P \right)$ tại $I$ thì $\frac{{d\left( {A;\left( P \right)} \right)}}{{d\left( {B;\left( P \right)} \right)}} = \frac{{AI}}{{BI}}$  để chỉ ra $d\left( {E;\left( {SBC} \right)} \right) = d\left( {A;\left( {SBC} \right)} \right)$

Từ đó tính $d\left( {A;\left( {SBC} \right)} \right)$ bằng cách dùng hệ thức lượng trong tam giác vuông.

Cách giải:

Cho tứ diện $SABC$ có $SA,AB,AC$ đôi một vuông góc, biết $SA = AB = AC = a$. Gọi $I$ là trung điểm của đoạn $BC$.

a) Chứng minh đường thẳng $SA$ vuông góc với mặt phẳng $\left( {ABC} \right)$. Chứng minh mặt phẳng $\left( {SAB} \right)$ vuông góc với mặt phẳng $\left( {SAC} \right)$.

Vì $\left\{ \begin{array}{l}SA \bot AB\\SA \bot AC\\AB \cap AC = \left\{ A \right\}\end{array} \right.$ $\Rightarrow SA \bot \left( {ABC} \right)$

Ta có $\left\{ \begin{array}{l}AB \bot AC\\AB \bot SA\\AC \cap SA = \left\{ A \right\}\end{array} \right.$ $\Rightarrow$ $AB \bot \left( {SAC} \right)$

Từ đó $\left\{ \begin{array}{l}AB \bot \left( {SAC} \right)\\AB \subset \left( {SAB} \right)\end{array} \right.$ $\Rightarrow \left( {SAB} \right) \bot \left( {SAC} \right)$

b) Chứng minh mặt phẳng $\left( {SAI} \right)$ vuông góc với mặt phẳng $\left( {SBC} \right)$.

Xét tam giác ABC cân tại A (do $AB = AC$) có $AI$ là trung tuyến nên $AI \bot BC$

Vì $SA \bot \left( {ABC} \right)$ (theo câu a) nên $SA \bot BC$

Ta có: $\left\{ \begin{array}{l}BC \bot AI\\BC \bot SA\\SA \cap AI = \left\{ A \right\}\end{array} \right.$ $\Rightarrow BC \bot \left( {SAI} \right)$

Từ đó $\left\{ \begin{array}{l}BC \bot \left( {SAI} \right)\\BC \subset \left( {SBC} \right)\end{array} \right.$ $\Rightarrow \left( {SAI} \right) \bot \left( {SBC} \right)$

c) Tính góc giữa hai mặt phẳng $\left( {SAB} \right)$ và $\left( {SAI} \right)$.

Vì $\left\{ \begin{array}{l}SA \bot \left( {ABC} \right)\\AI \subset \left( {ABC} \right)\end{array} \right.$ $\Rightarrow SA \bot AI$

Ta có:

$\left\{ \begin{array}{l}\left( {SAB} \right) \cap \left( {SAI} \right) = SA\\AI \bot SA,AI \subset \left( {SAI} \right)\\AB \bot SA,AB \subset \left( {SAB} \right)\end{array} \right.$

Suy ra góc giữa hai mặt phẳng $\left( {SAB} \right)$ và $\left( {SAI} \right)$ là góc giữa $AI$ và $AB$ hay là $\widehat {BAI}$

Vì tam giác $ABC$ vuông cân tại A có AI là đường trung tuyến nên AI cũng là đường phân giác góc A

Suy ra $\widehat {BAI} = \frac{1}{2}\widehat {BAC}$ $= \frac{1}{2}{90^0} = {45^0}$

Vậy góc giữa hai mặt phẳng $\left( {SAB} \right)$ và $\left( {SAI} \right)$ là ${45^0}.$

d) Trên tia đối của tia $IA$ lấy điểm $D$ sao cho $ID = 2IA$ và gọi $E$ là trung điểm của đoạn $SD$. Tính khoảng cách từ điểm $E$ đến mặt phẳng $\left( {SBC} \right)$ theo $a$.

Ta có DE giao với $\left( {SBC} \right)$ tại S nên $\frac{{d\left( {E;\left( {SBC} \right)} \right)}}{{d\left( {D;\left( {SBC} \right)} \right)}}$ $= \frac{{ES}}{{DS}} = \frac{1}{2}$$\Rightarrow d\left( {E;\left( {SBC} \right)} \right) = \frac{1}{2}d\left( {D;\left( {SBC} \right)} \right)$

Lại có $AD \cap \left( {SBC} \right)$ tại I nên $\frac{{d\left( {D;\left( {SBC} \right)} \right)}}{{d\left( {A;\left( {SBC} \right)} \right)}} = \frac{{DI}}{{AI}} = 2$ $\Rightarrow d\left( {D;\left( {SBC} \right)} \right) = 2d\left( {A;SBC} \right)$

Từ đó $d\left( {E;\left( {SBC} \right)} \right) = \frac{1}{2}.2d\left( {A;\left( {SBC} \right)} \right)$ $= d\left( {A;\left( {SBC} \right)} \right)$

Trong $\left( {SAI} \right)$ kẻ $AH \bot SI$ tại $H$

Ta có: $\left\{ \begin{array}{l}BC \bot \left( {SAI} \right)\left( {cmt} \right)\\AH \subset \left( {SAI} \right)\end{array} \right.$ $\Rightarrow BC \bot AH$

Từ đó $\left\{ \begin{array}{l}AH \bot BC\\AH \bot SI\\BC \cap SI = \left\{ I \right\}\end{array} \right.$ $\Rightarrow AH \bot \left( {SBC} \right)$ tại $H.$

Suy ra $d\left( {A;\left( {SBC} \right)} \right) = AH$

Vì $\Delta ABC$ vuông cân tại $A$ nên $AI = \frac{1}{2}BC$ $= \frac{1}{2}\sqrt {A{B^2} + A{C^2}}$ $= \frac{1}{2}\sqrt {{a^2} + {a^2}}  = \frac{{a\sqrt 2 }}{2}$

Xét tam giác $SAI$ vuông tại $A$, ta có: $\frac{1}{{A{H^2}}} = \frac{1}{{S{A^2}}} + \frac{1}{{A{I^2}}}$ $= \frac{1}{{{a^2}}} + \frac{1}{{{{\left( {\frac{{a\sqrt 2 }}{2}} \right)}^2}}} = \frac{3}{{{a^2}}}$

$\Rightarrow AH = \frac{a}{{\sqrt 3 }}$

Suy ra $d\left( {E;\left( {SBC} \right)} \right) = d\left( {A;\left( {SBC} \right)} \right)$$= AH = \frac{a}{{\sqrt 3 }}$

Vậy $d\left( {E;\left( {SBC} \right)} \right) = \frac{a}{{\sqrt 3 }}$.

HẾT

HocTot.Nam.Name.Vn