Đề thi học kì 1 môn toán lớp 7 năm 2019 - 2020 phòng GDĐT Thanh TrìGiải chi tiết đề thi học kì 1 môn toán lớp 7 năm 2019 - 2020 phòng GDĐT Thanh Trì với cách giải nhanh và chú ý quan trọng PHẦN I. TRẮC NGHIỆM: (2 điểm) Chọn chữ cái trước đáp án đúng Câu 1 : Kết quả của phép tính \({\left( {\dfrac{1}{3}} \right)^9}:{\left( {\dfrac{1}{9}} \right)^3}\) A. \({\left( {\dfrac{1}{3}} \right)^3}\) B. \({\left( { - \dfrac{1}{3}} \right)^3}\) C. \(\dfrac{1}{3}\) D. \( - \dfrac{1}{3}\) Câu 2 : Nếu \(\sqrt {x + 3} = 4\) thì \(x\) bằng: A. \(16\) B. \( \pm 13\) C. \(13\) D. \( \pm 169\) Câu 3 : Từ tỉ lệ thức \(\dfrac{a}{b} = \dfrac{c}{d}\,\,\left( {a,b,c,d \ne 0} \right)\) ta có thể suy ra A. \(\dfrac{a}{c} = \dfrac{d}{b}\,\) B. \(\dfrac{a}{d} = \dfrac{b}{c}\,\) C. \(\dfrac{b}{a} = \dfrac{d}{c}\,\) D. \(\dfrac{a}{b} = \dfrac{d}{c}\,\) Câu 4 : Điểm thuộc đồ thị hàm số \(y = - 5x\) là: A. \(\left( {1\,;\,\,3} \right)\) B. \(\left( {1\,;\,\, - 5} \right)\) C. \(\left( {\dfrac{1}{5}\,;\,\,1} \right)\) D. \(\left( {0\,;\,\,5} \right)\) Câu 5 : Cho đường thẳng \(c\)cắt hai đường thẳng \(a\) và \(b\) và trong các góc tạo thành có một cặp góc so le trong bằng nhau thì: A. \(a//b\) B. \(a\) cắt \(b\) C. \(a \bot b\) D. \(a\) trùng với \(b\) Câu 6 : Cho \(\Delta ABC\) có \(\angle A = 40^\circ ;\,\,\angle C = 80^\circ \). Góc ngoài của tam giác tại đỉnh \(B\) có số đo là: A. \(140^\circ \) B. \(100^\circ \) C. \(60^\circ \) D. \(120^\circ \) Câu 7 : Cho \(\Delta ABC\) và \(\Delta MNP\), biết \(\widehat B = \widehat N;\,\,\,\widehat A = \widehat P\). Cần thêm điều kiện gì để \(\Delta ABC = \Delta MNP\)? A. \(\angle C = \angle M\) B. \(AB = MP\) C. \(AC = MN\) D. \(BA = NP\) Câu 8 : Đường trung trực của đoạn thẳng \(MN\) là đường thẳng A. Vuông góc với \(MN\) B. Song song với \(MN\) C. Vuông góc với \(MN\) tại trung điểm của \(MN\) D. Cắt \(MN\) tại trung điểm của \(MN\) PHẦN II. TỰ LUẬN Bài 1: (1,0 điểm) Thực hiện phép tính: \(a)\,\,\dfrac{4}{{13}}.15\dfrac{3}{{41}} - \dfrac{4}{{13}}.2\dfrac{3}{{41}}\) \(b)\,\,\sqrt {25} .\left( {0,4 - 1\dfrac{1}{2}} \right):\left[ {{{\left( { - 2} \right)}^3}.\dfrac{{11}}{8}} \right]\) Bài 2: (1,0 điểm) a) Tìm \(x\) biết: \(\dfrac{3}{4} + \dfrac{1}{4}:x = 2\). b) Tìm \(x,y\) biết: \(3x = 2y\) và \(x - 2y = 8\) Bài 3: (2,0 điểm) Học sinh ba lớp 7 cần phải chăm sóc \(24\) cây xanh. Lớp 7A có \(32\) học sinh, lớp 7B có \(28\) học sinh, lớp 7C có \(36\) học sinh. Hỏi mỗi lớp phải chăm sóc bao nhiêu cây xanh biết số cây xanh tỉ lệ thuận với số học sinh. Bài 4: (3,5 điểm) Cho tam giác \(ABC\) có ba góc đều nhọn, \(AB < AC\). Lấy \(E\) là trung điểm của \(BC\). Trên tia \(AE\) lấy điểm \(D\) sao cho \(E\) là trung điểm của \(AD\). a) Chứng minh rằng: \(\Delta ABE = \Delta DCE\). b) Chứng minh: \(AC//BD\). c) Vẽ \(AH\) vuông góc với \(EC\) (\(H\) thuộc \(BC\)). Trên tia \(AH\) lấy điểm \(K\) sao cho \(H\) là trung điểm của \(AK\). Chứng minh rằng \(BD = AC = CK\). d) Chứng minh \(DK\) vuông góc với \(AH\). Bài 5: (0,5 điểm) Cho \(a + b + c = {a^2} + {b^2} + {c^2} = 1\) và \(\dfrac{x}{a} = \dfrac{y}{b} = \dfrac{z}{c}\) (với \(a \ne 0;\,\,b \ne 0;\,\,c \ne 0\)). Chứng minh rằng : \({\left( {x + y + z} \right)^2} = {x^2} + {y^2} + {z^2}\).
HƯỚNG DẪN GIẢI CHI TIẾT Thực hiện: Ban chuyên môn HocTot.Nam.Name.Vn PHẦN I: TRẮC NGHIỆM
Câu 1(TH): Phương pháp Sử dụng công thức \({a^m}:{a^n} = {a^{m - n}}\) Cách giải: \({\left( {\dfrac{1}{3}} \right)^9}:{\left( {\dfrac{1}{9}} \right)^3}\)\( = {\left( {\dfrac{1}{3}} \right)^9}:{\left( {\dfrac{1}{3}} \right)^6}\) \( = {\left( {\dfrac{1}{3}} \right)^{9 - 6}} = {\left( {\dfrac{1}{3}} \right)^3}\) Chọn A. Câu 2(VD): Phương pháp Sử dụng công thức \(\sqrt A = B\left( {B > 0} \right)\) thì \(A = {B^2}\) Cách giải: \(\sqrt {x + 3} = 4\) \(\begin{array}{l}x + 3 = {4^2}\\x + 3 = 16\\x = 16 - 3\\x = 13\end{array}\) Chọn C. Câu 3(NB): Phương pháp Sử dụng tính chất tỉ lệ thức \(\dfrac{a}{b} = \dfrac{c}{d}\). Cách giải: Từ tỉ lệ thức \(\dfrac{a}{b} = \dfrac{c}{d}\,\,\left( {a,b,c,d \ne 0} \right)\) ta có thể suy ra \(\dfrac{b}{a} = \dfrac{d}{c}\). Chọn C. Câu 4(TH): Phương pháp Thay lần lượt tọa độ các điểm vào hàm số. Cách giải: Đáp án A : Với \(x = 1\) thì \(y = - 5.1 = - 5 \ne 3\) nên điểm \(\left( {1;3} \right)\) không thuộc đồ thị hàm số. Đáp án B : Với \(x = 1\) thì \(y = - 5.1 = - 5\) nên điểm \(\left( {1; - 5} \right)\) thuộc đồ thị hàm số. Chọn B. Câu 5(NB): Phương pháp Sử dụng dấu hiệu nhận biết hai đường thẳng song song. Cách giải: Nếu đường thẳng \(c\)cắt hai đường thẳng \(a\) và \(b\) và trong các góc tạo thành có một cặp góc so le trong bằng nhau thì \(a//b\). Chọn A. Câu 6(NB: Phương pháp Góc ngoài của tam giác bằng tổng hai góc trong không kề với nó. Cách giải: Số đo góc ngoài tại đỉnh \(B\) của tam giác \(ABC\) là \({40^0} + {80^0} = {120^0}\). Chọn D. Câu 7(NB): Phương pháp Sử dụng trường hợp bằng nhau g-c-g : Nếu một cạnh và hai góc kề của tam giác này bằng một cạnh và hai góc kề của tam giác kia thì hai tam giác bằng nhau. Cách giải: Nếu \(\widehat B = \widehat N;\,\,\,\widehat A = \widehat P\) thì để \(\Delta ABC\) và \(\Delta MNP\) bằng nhau ta cần \(AB = NP\) Chọn D. Câu 8(NB): Phương pháp Đường trung trực của đoạn thẳng là đường thẳng vuông góc với đoạn thẳng tại trung điểm của nó. Cách giải: Đường trung trực của đoạn thẳng \(MN\) là đường thẳng vuông góc với \(MN\) tại trung điểm của \(MN\). Chọn C. PHẦN II: TỰ LUẬN Bài 1(VD): Phương pháp a) Sử dụng tính chất phân phối của phép nhân và cộng \(ab + ac = a\left( {b + c} \right)\). b) Đưa về phân số và tính toán. Cách giải: \(a)\,\,\dfrac{4}{{13}}.15\dfrac{3}{{41}} - \dfrac{4}{{13}}.2\dfrac{3}{{41}}\) \(\begin{array}{l} = \dfrac{4}{{13}}\left( {15\dfrac{3}{{41}} - 2\dfrac{3}{{41}}} \right)\\ = \dfrac{4}{{13}}.13\\ = 4\end{array}\) \(b)\,\,\sqrt {25} .\left( {0,4 - 1\dfrac{1}{2}} \right):\left[ {{{\left( { - 2} \right)}^3}.\dfrac{{11}}{8}} \right]\) \(\begin{array}{l} = 5.\left( {\dfrac{2}{5} - \dfrac{3}{2}} \right):\left( { - 8.\dfrac{{11}}{8}} \right)\\ = 5.\left( {\dfrac{4}{{10}} - \dfrac{{15}}{{10}}} \right):\left( { - 11} \right)\\ = 5.\dfrac{{ - 11}}{{10}}.\dfrac{{ - 1}}{{11}}\\ = \dfrac{1}{2}\end{array}\) Bài 2(VD): Phương pháp a) Sử dụng quy tắc chuyển vế đổi dấu. b) Sử dụng tính chất dãy tỉ số bằng nhau \(\dfrac{a}{x} = \dfrac{b}{y} = \dfrac{{ma \pm nb}}{{mx \pm ny}}\) Cách giải: a) Tìm \(x\) biết: \(\dfrac{3}{4} + \dfrac{1}{4}:x = 2\). \(\begin{array}{l}\dfrac{1}{4}:x = 2 - \dfrac{3}{4}\\\dfrac{1}{4}:x = \dfrac{5}{4}\\x = \dfrac{1}{4}:\dfrac{5}{4}\\x = \dfrac{1}{5}\end{array}\) b) Tìm \(x,y\) biết: \(3x = 2y\)và \(x - 2y = 8\) \(3x = 2y \Rightarrow \dfrac{x}{2} = \dfrac{y}{3}\) Áp dụng tính chất dãy tỉ số bằng nhau ta có : \(\dfrac{x}{2} = \dfrac{y}{3} = \dfrac{{x - 2y}}{{2 - 2.3}} = \dfrac{8}{{ - 4}} = - 2\) \(\begin{array}{l} \Rightarrow \dfrac{x}{2} = - 2 \Rightarrow x = \left( { - 2} \right).2 = - 4\\\dfrac{y}{3} = - 2 \Rightarrow y = \left( { - 2} \right).3 = - 6\end{array}\) Vậy \(x = - 4,y = - 6\). Bài 3(VD): Phương pháp Gọi số cây phải chăm sóc của 3 lớp lần lượt là \(x,y,z\) Thiết lập mối quan hệ \(x,y,z\) và tìm \(x,y,z\). Cách giải: Gọi số cây phải chăm sóc của 3 lớp lần lượt là \(x,y,z\) (\(x,y,z \in \mathbb{N},x,y,z < 24\)) Vì tổng số cây ba lớp là \(24\) cây nên \(x + y + z = 24\) Số cây tỉ lệ với số học sinh nên \(\dfrac{x}{{32}} = \dfrac{y}{{28}} = \dfrac{z}{{36}}\) Áp dụng tính chất dãy tỉ số bằng nhau ta có: \(\dfrac{x}{{32}} = \dfrac{y}{{28}} = \dfrac{z}{{36}}\)\( = \dfrac{{x + y + z}}{{32 + 28 + 36}} = \dfrac{{24}}{{96}} = \dfrac{1}{4}\) \( \Rightarrow x = 32.\dfrac{1}{4} = 8\) \(y = 28.\dfrac{1}{4} = 7\) \(z = 36.\dfrac{1}{4} = 9\) Vậy lớp \(7A\) trồng \(8\) cây, \(7B\) trồng \(7\) cây, \(7C\) trồng \(9\) cây. Bài 4(VD): Phương pháp a) Sử dụng trường hợp bằng nhau cạnh-góc-cạnh. b) Chứng minh \(\Delta ACE = \Delta DBE\left( {c - g - c} \right)\) suy ra hai góc tương ứng bằng nhau rồi suy ra song song. c) Chứng minh \(\Delta CAH = \Delta CKH\left( {c - g - c} \right)\) suy ra hai cạnh bằng nhau tương ứng. d) Chứng minh \(EA = EK = ED\) suy ra các cặp góc bằng nhau. Sử dụng tính chất tổng ba góc của một tam giác suy ra góc \(\angle AKD\) vuông. Cách giải:
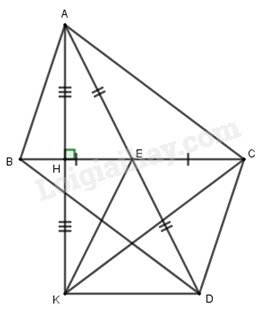
a) Chứng minh rằng: \(\Delta ABE = \Delta DCE\). Xét \(\Delta ABE\) và \(\Delta DCE\) có : \(EB = EC\) (\(E\) là trung điểm \(BC\)) \(EA = ED\) (\(E\) là trung điểm \(AD\)) \(\angle AEB = \angle DEC\) (đối đỉnh) \( \Rightarrow \Delta ABE = \Delta DCE\left( {c - g - c} \right)\) b) Chứng minh: \(AC//BD\). Xét \(\Delta ACE\) và \(\Delta DBE\) có : \(EB = EC\) (\(E\) là trung điểm \(BC\)) \(EA = ED\) (\(E\) là trung điểm \(AD\)) \(\angle AEC = \angle DEB\) (đối đỉnh) \( \Rightarrow \Delta ACE = \Delta DBE\left( {c - g - c} \right)\) \( \Rightarrow \angle ACE = DBE\) (góc tương ứng) Mà hai góc ở vị trí so le trong nên \(AC//BD\) (đpcm) c) Vẽ \(AH\) vuông góc với \(EC\) (\(H\) thuộc \(BC\)). Trên tia \(AH\) lấy điểm \(K\) sao cho \(H\) là trung điểm của \(AK\). Chứng minh rằng \(BD = AC = CK\). Ta có : \(\Delta ACE = \Delta DBE\left( {cmt} \right)\)\( \Rightarrow BD = AC\) (cạnh tương ứng) (1) Xét \(\Delta CAH\) và \(\Delta CKH\) có : \(CH\) chung \(\angle CHA = \angle CHK = {90^0}\) \(HA = HK\left( {gt} \right)\) \( \Rightarrow \Delta CAH = \Delta CKH\left( {c - g - c} \right)\) \( \Rightarrow CA = CK\) (2) Từ (1) và (2) suy ra \(AC = BD = CK\) (đpcm) d) Chứng minh \(DK\) vuông góc với \(AH\). Nối \(E\) với \(K\). Xét \(\Delta EAH\) và \(\Delta EKH\) có : \(EH\) chung \(\angle EHA = \angle EHK = {90^0}\) \(HA = HK\left( {gt} \right)\) \( \Rightarrow \Delta EAH = \Delta EKH\left( {c - g - c} \right)\) \( \Rightarrow \angle EAH = \angle EKH\) (góc t/ư) (3) \(EK = EA\) (cạnh t/ư), mà \(EA = ED\left( {gt} \right)\) \( \Rightarrow EK = ED\) \( \Rightarrow \Delta EKD\) cân tại \(E\) \( \Rightarrow \angle EKD = \angle EDK\) (t/c) (4) Từ (3) và (4) suy ra \(\angle EAK + \angle EDK = \angle EKA + \angle EKD = \angle AKD\) Tam giác \(AKD\) có : \(\angle EAK + \angle EDK + \angle AKD = {180^0}\) \(\begin{array}{l} \Rightarrow \angle AKD + \angle AKD = {180^0}\\ \Rightarrow 2\angle AKD = {180^0}\\ \Rightarrow \angle AKD = {180^0}:2 = {90^0}\end{array}\) Vậy \(AK \bot KD\) (đpcm). Bài 5(VDC): Phương pháp Sử dụng tính chất dãy tỉ số bằng nhau \(\dfrac{x}{a} = \dfrac{y}{b} = \dfrac{z}{c} = \dfrac{{x + y + z}}{{a + b + c}}\) Cách giải: Theo giả thiết ta có : \(\dfrac{x}{a} = \dfrac{y}{b} = \dfrac{z}{c}\). Áp dụng dãy tỉ số bằng nhau ta có: \(\dfrac{x}{a} = \dfrac{y}{b} = \dfrac{z}{c} = \dfrac{{x + y + z}}{{a + b + c}}\)\( = \dfrac{{x + y + z}}{1} = x + y + z\) Ta có : \({\left( {x + y + z} \right)^2} = {\left( {\dfrac{x}{a}} \right)^2} = {\left( {\dfrac{y}{b}} \right)^2} = {\left( {\dfrac{z}{c}} \right)^2}\) \( = \dfrac{{{x^2}}}{{{a^2}}} = \dfrac{{{y^2}}}{{{b^2}}} = \dfrac{{{z^2}}}{{{c^2}}}\) \( = \dfrac{{{x^2} + {y^2} + {z^2}}}{{{a^2} + {b^2} + {c^2}}} = \dfrac{{{x^2} + {y^2} + {z^2}}}{1}\) \( = {x^2} + {y^2} + {z^2}\) Vậy \({\left( {x + y + z} \right)^2} = {x^2} + {y^2} + {z^2}\) (đpcm). HocTot.Nam.Name.Vn
|