Đề thi học kì 1 môn toán lớp 7 năm 2019 - 2020 trường THCS Nguyễn Công Trứ

Bài 1. (1,5 điểm)

a) Tính hợp lý: $\dfrac{1}{4} + \dfrac{3}{4}.19\dfrac{1}{3} - \dfrac{3}{4}.39\dfrac{1}{3}$

b) Thực hiện phép tính: $\left[ {\sqrt {\dfrac{4}{9}}  + {{\left( { - \dfrac{1}{2}} \right)}^2}} \right]:0,75 + 1\dfrac{1}{3}.\left| {1 - \dfrac{{11}}{{12}}} \right|$

Bài 2. (1,5 điểm)  Tìm $x$ biết: 

$a)\,\,\dfrac{3}{4}x + \dfrac{1}{2} = 5$

$b)\,\,1\dfrac{1}{4} - \left| {x + \dfrac{5}{6}} \right| = \dfrac{{ - 5}}{7}.\dfrac{{21}}{6}$

$c)\,\,\left( {{x^2} + \sqrt {16} } \right)\left( {\left| x \right| - \dfrac{1}{3}} \right) = 0$

Bài 3. (1 điểm) Cho hàm số $y = f\left( x \right) = 2{x^2} + 3$.

a) Tính $f\left( 0 \right),f\left( {\dfrac{1}{2}} \right)$

b) Tìm $x$ biết $f\left( x \right) = 11$.

Bài 4. (2 điểm) Sàn nhà của bác An là hình chữ nhật có độ dài hai cạnh tỉ lệ với 3; 4 và chu vi là $28$ mét.

a) Tìm chiều dài hai cạnh của sàn nhà bác An.

b) Bác An dự định mua gạch men để lát lại sàn nhà. Của hàng báo giá mỗi mét vuông gạch là 300.000 đồng. Em hãy tính xem số tiền phải trả để mua gạch men là bao nhiêu?

Bài 5. (3,5 điểm) Cho $\Delta ABC$ $\left( {AB < AC} \right)$. $AE$ là phân giác của góc $\widehat {BAC}$ $\left( {E \in BC} \right)$. Trên cạnh $AC$ lấy điểm $M$ sao cho $AM = AB$.

a) Chứng minh $\Delta ABE = \Delta AME$.

b) $AE$ cắt $BM$ tại điểm $I$. Chứng minh $I$ là trung điểm của $BM$.

c) Trên tia đối của tia $EM$ lấy điểm $N$ sao cho $EN = EC$. Chứng minh $\Delta ENB = \Delta ECM$.

d) Chứng minh 3 điểm $A,B,N$ thẳng hàng.

Bài 6. (0,5 điểm) Cho $\dfrac{{3z - 4y}}{5} = \dfrac{{5y - 3x}}{4} = \dfrac{{4x - 5z}}{3}$ và ${x^2} - {z^2} = 36$. Hãy tìm $x,y,z$.

HẾT

HƯỚNG DẪN GIẢI CHI TIẾT

Thực hiện: Ban chuyên môn HocTot.Nam.Name.Vn

Bài 1 (VD):

Phương pháp:

Nhóm các số hạng thích hợp để được tổng là số tròn trăm, tròn chục,…

Thứ tự thực hiện phép tính:

- Có ngoặc: trong ngoặc trước, ngoài ngoặc sau.

- Không có ngoặc: Lũy thừa, nhân chia, công trừ.

Cách giải:

a) Tính hợp lý:

$\dfrac{1}{4} + \dfrac{3}{4}.19\dfrac{1}{3} - \dfrac{3}{4}.39\dfrac{1}{3}$

$\begin{array}{l} = \dfrac{1}{4} + \dfrac{3}{4}\left( {19\dfrac{1}{3} - 39\dfrac{1}{3}} \right)\\ = \dfrac{1}{4} + \dfrac{3}{4}.\left( { - 20} \right)\\ = \dfrac{1}{4} - 15\\ = \dfrac{1}{4} - \dfrac{{60}}{4}\\ =  - \dfrac{{59}}{4}\end{array}$

b) Thực hiện phép tính:

$\left[ {\sqrt {\dfrac{4}{9}}  + {{\left( { - \dfrac{1}{2}} \right)}^2}} \right]:0,75 + 1\dfrac{1}{3}.\left| {1 - \dfrac{{11}}{{12}}} \right|$

$\begin{array}{l} = \left[ {\dfrac{2}{3} + \dfrac{1}{4}} \right]:\dfrac{3}{4} + \dfrac{4}{3}.\dfrac{1}{{12}}\\ = \left( {\dfrac{8}{{12}} + \dfrac{3}{{12}}} \right).\dfrac{4}{3} + \dfrac{1}{9}\\ = \dfrac{{11}}{{12}}.\dfrac{4}{3} + \dfrac{1}{9}\\ = \dfrac{{11}}{9} + \dfrac{1}{9}\\ = \dfrac{{12}}{9} = \dfrac{4}{3}\end{array}$

Bài 2 (VD):

Phương pháp:

a) Áp dụng quy tắc chuyển vế đổi dấu.

b) Sử dụng kiến thức: $\left| A \right| = B > 0$ thì $A = B$ hoặc $A =  - B$.

c) Sử dụng kiến thức: $AB = 0$ thì $A = 0$ hoặc $B = 0$.

Cách giải:

$a)\,\,\dfrac{3}{4}x + \dfrac{1}{2} = 5$

$\begin{array}{l}\dfrac{3}{4}x = 5 - \dfrac{1}{2}\\\dfrac{3}{4}x = \dfrac{9}{2}\\x = \dfrac{9}{2}:\dfrac{3}{4}\\x = \dfrac{9}{2}.\dfrac{4}{3}\\x = 6\end{array}$

$b)\,\,1\dfrac{1}{4} - \left| {x + \dfrac{5}{6}} \right| = \dfrac{{ - 5}}{7}.\dfrac{{21}}{6}$

$\begin{array}{l}\dfrac{5}{4} - \left| {x + \dfrac{5}{6}} \right| =  - \dfrac{5}{2}\\\left| {x + \dfrac{5}{6}} \right| = \dfrac{5}{4} + \dfrac{5}{2}\\\left| {x + \dfrac{5}{6}} \right| = \dfrac{{15}}{4}\end{array}$

+) TH1: $x + \dfrac{5}{6} = \dfrac{{15}}{4}$

$\begin{array}{l}x = \dfrac{{15}}{4} - \dfrac{5}{6}\\x = \dfrac{{35}}{{12}}\end{array}$

+) TH2: $x + \dfrac{5}{6} =  - \dfrac{{15}}{4}$

$\begin{array}{l}x =  - \dfrac{{15}}{4} - \dfrac{5}{6}\\x =  - \dfrac{{55}}{{12}}\end{array}$

Vậy $x = \dfrac{{35}}{{12}}$ hoặc $x =  - \dfrac{{55}}{{12}}$.

$c)\,\,\left( {{x^2} + \sqrt {16} } \right)\left( {\left| x \right| - \dfrac{1}{3}} \right) = 0$

$\left( {{x^2} + 4} \right)\left( {\left| x \right| - \dfrac{1}{3}} \right) = 0$

TH1: ${x^2} + 4 = 0$

$\begin{array}{l}{x^2} = 0 - 4\\{x^2} =  - 4\end{array}$

Không có giá trị nào của $x$ thỏa mãn vì ${x^2} \ge 0$ với mọi $x$ và $- 4 < 0$.

TH2: $\left| x \right| - \dfrac{1}{3} = 0$

$\begin{array}{l}\left| x \right| = \dfrac{1}{3}\\x =  \pm \dfrac{1}{3}\end{array}$

Vậy $x =  \pm \dfrac{1}{3}$.

Bài 3 (VD):

Phương pháp:

a) Thay các giá trị của $x$ vào tính giá trị của hàm số.

b) Cho $f\left( x \right) = 11$ và tìm $x$.

Cách giải:

a) Tính $f\left( 0 \right),f\left( {\dfrac{1}{2}} \right)$

Với $x = 0$ thì $f\left( 0 \right) = {2.0^2} + 3 = 3$.

Với $x = \dfrac{1}{2}$ thì $f\left( {\dfrac{1}{2}} \right) = 2.{\left( {\dfrac{1}{2}} \right)^2} + 3 = \dfrac{7}{2}$.

Vậy $f\left( 0 \right) = 3;f\left( {\dfrac{1}{2}} \right) = \dfrac{7}{2}$.

b) Tìm $x$ biết $f\left( x \right) = 11$.

Khi $f\left( x \right) = 11$ ta có:

$\begin{array}{l}2{x^2} + 3 = 11\\2{x^2} = 11 - 3\\2{x^2} = 8\\{x^2} = 4\\x =  \pm 2\end{array}$

Vậy với $x =  \pm 2$ thì $f\left( x \right) = 11$.

Bài 4 (VD):

Phương pháp:

a) Gọi chiều dài, chiều rộng là $x,y$.

Lập luận thiết lập mối quan hệ của $x,y$ dựa vào điều kiện bài cho.

Sử dụng tính chất của dãy tỉ số bằng nhau: $\dfrac{a}{b} = \dfrac{c}{d} = \dfrac{{a + c}}{{b + d}}$.

b) Tính diện tích mặt sàn, từ đó suy ra số tiền cần trả.

Cách giải:

a) Tìm chiều dài hai cạnh của sàn nhà bác An.

Gọi chiều dài, chiều rộng sàn nhà lần lượt là $x,y$ $\left( {x > y > 0} \right)$.

Nửa chu vi hình chữ nhật là: $28:2 = 14\left( m \right)$.

Do đó $x + y = 14$.

Vì hai cạnh tỉ lệ với $3;4$ nên $\dfrac{x}{4} = \dfrac{y}{3}$ (do $x > y$)

Áp dụng tính chất của dãy tỉ số bằng nhau ta có:

$\dfrac{x}{4} = \dfrac{y}{3} = \dfrac{{x + y}}{{4 + 3}} = \dfrac{{14}}{7} = 2$

$\begin{array}{l} \Rightarrow x = 4.2 = 8\left( m \right)\\y = 3.2 = 6\left( m \right)\end{array}$

Vậy chiều rộng sàn nhà là $6m$ và chiều dài sàn nhà là $8m$.

b) Bác An dự định mua gạch men để lát lại sàn nhà. Của hàng báo giá mỗi mét vuông gạch là 300.000 đồng. Em hãy tính xem số tiền phải trả để mua gạch men là bao nhiêu?

Diện tích sàn nhà là: $6.8 = 48\left( {{m^2}} \right)$.

Số tiền phải trả là: $48.300000 = 14400000$ (đồng)

Vậy bác An phải trả $14400000$ đồng mua gạch men.

Bài 5 (VD):

Phương pháp:

a) Chứng minh hai tam giác bằng nhau theo trường hợp cạnh – góc – cạnh.

b) Chứng minh hai tam giác $\Delta ABI$ và $\Delta AMI$ bằng nhau theo trường hợp cạnh – góc – cạnh.

Từ đó suy ra hai cạnh bằng nhau tương ứng.

c) Chứng minh hai tam giác $\Delta ENB$ và $\Delta ECM$ bằng nhau theo trường hợp cạnh – góc – cạnh.

d) Sử dụng các tam giác bằng nhau ở hai câu a, c suy ra các cặp góc tương ứng bằng nhau.

Chứng minh ba điểm $A,B,N$ thẳng hàng bằng cách chứng minh $\widehat {ABE} + \widehat {NBE} = {180^0}$.

Cách giải:

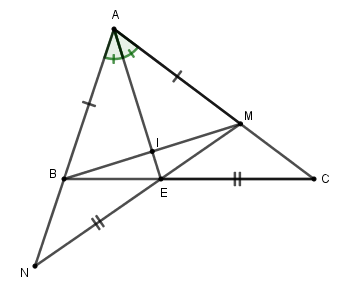
a) Chứng minh $\Delta ABE = \Delta AME$.

Xét $\Delta ABE$ và $\Delta AME$ có:

$AB = AM\left( {gt} \right)$

$\widehat {BAE} = \widehat {MAE}$ ($AE$ là tia phân giác góc $\widehat {BAC}$)

Chung $AE$

$\Rightarrow \Delta ABE = \Delta AME\left( {c - g - c} \right)$ (đpcm).

b) $AE$ cắt $BM$ tại điểm $I$. Chứng minh $I$ là trung điểm của $BM$.

Xét $\Delta ABI$ và $\Delta AMI$ có:

$AB = AM\left( {gt} \right)$

$\widehat {BAE} = \widehat {MAE}$ ($AE$ là tia phân giác góc $\widehat {BAC}$)

Chung $AI$

$\Rightarrow \Delta ABI = \Delta AMI\left( {c - g - c} \right)$.

$\Rightarrow BI = MI$ (cạnh tương ứng)

Do đó $I$ là trung điểm của $BM$ (đpcm).

c) Trên tia đối của tia $EM$ lấy điểm $N$ sao cho $EN = EC$. Chứng minh $\Delta ENB = \Delta ECM$.

Từ câu a, $\Delta ABE = \Delta AME$$\Rightarrow BE = ME$ (cạnh tương ứng)

Xét $\Delta ENB$ và $\Delta ECM$ có:

$EN = EC\left( {gt} \right)$

$\widehat {BEN} = \widehat {MEC}$ (đối đỉnh)

$EB = EM\left( {cmt} \right)$

$\Rightarrow \Delta ENB = \Delta ECM\left( {c - g - c} \right)$ (đpcm).

d) Chứng minh 3 điểm $A,B,N$ thẳng hàng.

Từ câu a, $\Delta ABE = \Delta AME$$\Rightarrow \widehat {ABE} = \widehat {AME}$ (góc tương ứng)  (1)

Từ câu c, $\Delta ENB = \Delta ECM$ $\Rightarrow \widehat {NBE} = \widehat {CME}$ (góc tương ứng)  (2)

Từ (1) và (2) suy ra: $\widehat {ABE} + \widehat {NBE} = \widehat {AME} + \widehat {CME}$

Mà $\widehat {AME} + \widehat {CME} = {180^0}$ (hai góc kề bù)

Nên $\widehat {ABE} + \widehat {NBE} = {180^0}$.

Vậy ba điểm $A,B,N$ thẳng hàng (đpcm).

Bài 6(VDC):

Phương pháp:

Nhân cả tử và mẫu của phân thức đầu tiên với $5$, phân thức thứ hai với $4$ và phân thức thứ ba với $3$.

Sử dụng tính chất dãy tỉ số bằng nhau suy ra dãy tỉ số mới.

Cách giải:

Ta có :

$\dfrac{{3z - 4y}}{5} = \dfrac{{5y - 3x}}{4} = \dfrac{{4x - 5z}}{3}$

$\Rightarrow \dfrac{{5\left( {3z - 4y} \right)}}{{5.5}} = \dfrac{{4.\left( {5y - 3x} \right)}}{{4.4}} = \dfrac{{3\left( {4x - 5z} \right)}}{{3.3}}$

$\Rightarrow \dfrac{{15z - 20y}}{{25}} = \dfrac{{20y - 12x}}{{16}} = \dfrac{{12x - 15z}}{9}$

$= \dfrac{{15z - 20y + 20y - 12x + 12x - 15z}}{{25 + 16 + 9}}$ $= 0$

Suy ra  $15z - 20y = 0 \Rightarrow 15z = 20y$ $\Rightarrow \dfrac{z}{4} = \dfrac{y}{3}$

$20y - 12x = 0$ $\Rightarrow 20y = 12x \Rightarrow \dfrac{y}{3} = \dfrac{x}{5}$

Suy ra $\dfrac{x}{5} = \dfrac{y}{3} = \dfrac{z}{4} = k$$\Rightarrow \left\{ \begin{array}{l}x = 5k\\y = 3k\\z = 4k\end{array} \right.$

Mà ${x^2} - {z^2} = 36$ nên ${\left( {5k} \right)^2} - {\left( {4k} \right)^2} = 36$

$\begin{array}{l}25{k^2} - 16{k^2} = 36\\9{k^2} = 36\\{k^2} = 4\\k =  \pm 2\end{array}$

Nếu $k = 2$ thì $\left\{ \begin{array}{l}x = 5.2 = 10\\y = 3.2 = 6\\z = 4.2 = 8\end{array} \right.$

Nếu $k =  - 2$ thì $\left\{ \begin{array}{l}x = 5.\left( { - 2} \right) =  - 10\\y = 3.\left( { - 2} \right) =  - 6\\z = 4.\left( { - 2} \right) =  - 8\end{array} \right.$

Vậy $\left( {x;y;z} \right) \in \left\{ {\left( {10;6;8} \right),\left( { - 10; - 6; - 8} \right)} \right\}$.

HẾT

HocTot.Nam.Name.Vn