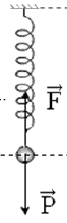Giải đề thi học kì 1 lý lớp 10 năm 2020 - 2021 trường đại học Công Nghiệp Thực Phẩm TP HCM trung tâm GDPT

Đề bài

Câu 1 (2 điểm)

Phát biểu và viết công thức định luật vạn vật hấp dẫn. Nêu rõ tên gọi, đơn vị từng đại lượng trong công thức.

Câu 2 (2 điểm)

Phát biểu và viết công thức định luật Húc. Nêu rõ tên gọi, đơn vị từng đại lượng trong công thức.

Câu 3 (1 điểm)

Tính lực hấp dẫn giữa hai tàu thủy, biết mỗi tàu có khối lượng 35000 tấn và ở cách nhau 0,2 km.

Câu 4 (1 điểm)

Một lò xo khối lượng không đáng kể được treo thẳng đứng. Treo vào đầu dưới của lò xo một vật có khối lượng 200g thì lò xo dãn ra 2 cm. Lấy \(g = 10m/{s^2}\). Tính độ cứng của lò xo.

Câu 5 (3 điểm)

Một vật có khối lượng 10kg ban đầu đứng yên được kéo bằng một lực không đổi \(F = 20N\) theo phương ngang, làm vật trượt trên một mặt sàn nằm ngang. Biết hệ số ma sát trượt giữa vật và mặt sàn là 0,1. Lấy \(g = 10m/{s^2}\).

a) Tính lực ma sát trượt giữa vật và sàn.

b) Tính gia tốc của vật

c) Sau khi đi được 5s thì lực F ngừng tác dụng. Tính quãng đường vật đi được từ lúc lực F ngừng tác dụng đến khi vật dừng lại.

Câu 6 (1 điểm)

Một lực có độ lớn 20N tác dụng lên một vật rắn quay quanh một trục cố định, biết khoảng cách từ giá của lực đến trục quay là 30cm. Momen của lực tác dụng lên vật có trị là bao nhiêu?

Lời giải chi tiết

HƯỚNG DẪN GIẢI CHI TIẾT

Thực hiện: Ban chuyên môn HocTot.Nam.Name.Vn

Câu 1:

Phương pháp

Vận dụng lý thuyết bài lực hấp dẫn.

Cách giải

- Nội dung định luật vạn vật hấp dẫn:

Lực hấp dẫn giữa hai chất điểm bất kì tỉ lệ thuận với tích hai khối lượng của chúng và tỉ lệ nghịch với bình phương khoảng cách giữa chúng.

- Công thức:

\({F_{h{\rm{d}}}} = G\frac{{{m_1}{m_2}}}{{{r^2}}}\)

Trong đó:

\({m_1},{m_2}\): là khối lượng của hai chất điểm (kg)

\(r\): là khoảng cách giữa hai chất điểm (m)

\(G = 6,{67.10^{ - 11}}N.{m^2}/k{g^2}\): hằng số hấp dẫn

\({F_{h{\rm{d}}}}\): là lực hấp dẫn (N)

Câu 2:

Phương pháp

Vận dụng lý thuyết bài “Lực đàn hồi của lò xo. Định luật Húc”.

Cách giải

- Nội dung định luật Húc:

Trong giới hạn đàn hồi, độ lớn của lực đàn hồi của lò xo tỉ lệ thuận với độ biến dạng của lò xo.

- Công thức:

\({F_{dh}} = k\left| {\Delta l} \right|\)

Trong đó:

\({F_{dh}}\): là lực đàn hồi (N)

\(k\): là độ cứng (hay hệ số đàn hồi) của lò xo (N/m)

\(\Delta l\): là độ biến dạng của lò xo (m)

Câu 3:

Phương pháp

Áp dụng biểu thức của lực hấp dẫn: \({F_{h{\rm{d}}}} = G\frac{{{m_1}{m_2}}}{{{r^2}}}\)

Cách giải

Lực hấp dẫn giữa hai tàu thủy là:

\({F_{h{\rm{d}}}} = G\frac{{{m_1}{m_2}}}{{{r^2}}} = 6,{67.10^{ - 11}}.\frac{{{{\left( {{{35000.10}^3}} \right)}^2}}}{{{{\left( {0,{{2.10}^3}} \right)}^2}}}\\ = 2,043\left( N \right)\)

Câu 4:

Phương pháp

Áp dụng biểu thức định luật Húc \({F_{dh}} = k\left| {\Delta l} \right|\)

Cách giải

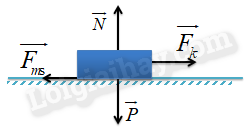
Lò xo treo thẳng đứng, vật gắn vào lò xo chịu tác dụng của trọng lực \(\overrightarrow P \) và lực đàn hồi \(\overrightarrow {{F_{dh}}} \) có phương và chiều như hình vẽ. Hai lực này cân bằng nhau.

Suy ra:

\({F_{dh}} = P\)

\( \Leftrightarrow k\left| {\Delta l} \right| = mg\)

\( \Leftrightarrow k = \frac{{mg}}{{\left| {\Delta l} \right|}} = \frac{{{{200.10}^{ - 3}}.10}}{{{{2.10}^{ - 2}}}} = 100\left( {N/m} \right)\)

Vậy độ cứng k = 100 N/m

Câu 5:

Phương pháp

- Áp dụng định luật II Niuton

- Công thức độ lớn lực ma sát trượt \({F_{m{\rm{s}}}} = \mu N\)

- Các công thức của chuyển động thẳng biến đổi đều.

Cách giải

Các lực tác dụng lên vật gồm: \(\overrightarrow {{F_{m{\rm{s}}}}} ,\overrightarrow {{F_k}} ,\overrightarrow N ,\overrightarrow P \) có phương và chiều như hình vẽ.

Phương trình định luật II Niutơn viết cho vật là:

\(\overrightarrow {{F_{m{\rm{s}}}}}  + \overrightarrow {{F_k}}  + \overrightarrow N  + \overrightarrow P  = m\overrightarrow a \) (*)

a)

Chọn chiều dương cùng chiều chuyển động. Chiếu phương trình (*) lên chiều dương ta được:

\(\left\{ \begin{array}{l}{F_k} - {F_{m{\rm{s}}}} = ma\\N - P = 0 \Leftrightarrow N = P = mg\end{array} \right.\)

Lực ma sát trượt giữa vật và sàn là:

\({F_{m{\rm{s}}}} = \mu N = \mu mg = 0,1.10.10 = 10N\)

b)

Ta có: \({F_k} - {F_{m{\rm{s}}}} = ma\)

\( \Leftrightarrow a = \frac{{{F_k} - {F_{m{\rm{s}}}}}}{m} = \frac{{20 - 10}}{{10}} = 1\left( {m/{s^2}} \right)\)

c)

Khi lực F ngừng tác dụng thì: \( - {F_{m{\rm{s}}}} = ma' \Rightarrow a' = \frac{{ - {F_{m{\rm{s}}}}}}{m} = \frac{{ - 10}}{{10}} =  - 1\left( {m/{s^2}} \right)\)

Vận tốc của vật là: \({v_1} = {v_0} + at = 0 + 1.5 = 5\left( {m/s} \right)\) (ban đầu vật đứng yên nên v₀ = 0)

Quãng đường vật đi được từ lúc F ngừng tác dụng đến khi vật dừng lại là:

Gọi v₂ là vận tốc khi vật dừng lại => v₂ = 0.

Áp dụng công thức:

\(v_2^2 - v_1^2 = 2{\rm{a'}}s \Rightarrow s = \frac{{v_2^2 - v_1^2}}{{2{\rm{a'}}}} = \frac{{{0^2} - {5^2}}}{{2.\left( { - 1} \right)}} = 12,5m\)

Kết luận

a) \({F_{m{\rm{s}}}} = 10N\)

b) Gia tốc \(a = 1m/{s^2}\)

c) \(s = 12,5m\)

Câu 6:

Phương pháp

Áp dụng công thức mômen lực: M = F.d

Cách giải

Mômen của lực tác dụng lên vật có giá trị là:

\(M = F.d = 20.0,3 = 6\left( {N.m} \right)\)

HocTot.Nam.Name.Vn