Giải câu hỏi trắc nghiệm trang 79, 80 vở thực hành Toán 8

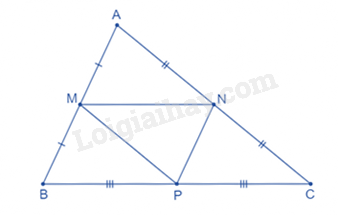
Câu 1 trang 79

Cho tam giác ABC. Gọi H, K lần lượt là trung điểm của AC, BC. Biết HK = 3,5 cm. Độ dài AB bằng

A. 3,5 cm.

B. 7 cm.

C. 10 cm.

D. 15 cm.

Phương pháp giải:

Dựa vào tính chất đường trung bình của tam giác.

Lời giải chi tiết:

Vì H, K lần lượt là trung điểm của AC, BC nên HK là đường trung bình của tam giác ABC suy ra \(HK = \frac{1}{2}AB.\).

Do đó AB = 2HK = 2 . 3,5 = 7 (cm).

Vậy AB = 7 cm.
=> Chọn đáp án B.

Câu 2 trang 79

Cho tam giác ABC có chu vi là 32 cm. Gọi M, N, P lần lượt là trung điểm của các cạnh AB, AC, BC. Chu vi của tam giác MNP là

A. 8 cm.

B. 64 cm.

C. 30 cm.

D. 16 cm.

Phương pháp giải:

Sử dụng tính chất đường trung bình của tam giác, công thức tính chu vi tam giác.

Lời giải chi tiết:

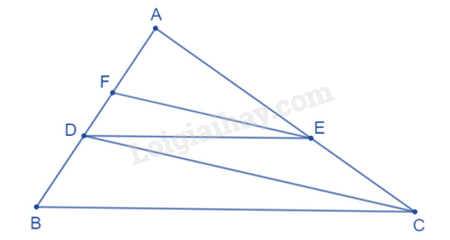
• Vì M, N lần lượt là trung điểm của các cạnh AB, AC nên MN là đường trung bình của tam giác ABC suy ra \(MN = \frac{1}{2}BC.\)

• Vì N, P lần lượt là trung điểm của các cạnh AC, BC nên NP là đường trung bình của tam giác ABC suy ra \(NP = \frac{1}{2}AB.\)

• Vì M, P lần lượt là trung điểm của các cạnh AB, BC nên MP là đường trung bình của tam giác ABC suy ra \(MP = \frac{1}{2}AC.\)

Chu vi tam giác ABC bằng: AB + BC + CA = 32 (cm).

Chu vi tam giác MNP bằng:

\(\begin{array}{l}MN + NP + MP = \frac{1}{2}BC + \frac{1}{2}AB + \frac{1}{2}AC\\ = \frac{1}{2}\left( {AB + BC + CA} \right) = \frac{1}{2}.32 = 16\,\,\left( {cm} \right).\end{array}\)

Vậy chu vi tam giác MNP bằng 16 cm.

=> Chọn đáp án D.

Câu 3 trang 80

Cho tam giác ABC có AB = 9 cm, D là điểm thuộc cạnh AB sao cho AD = 6 cm. Kẻ DE song song với BC (E thuộc AC), kẻ EF song song với CD (F thuộc AB). Độ dài AF bằng

A. 4 cm.

B. 5 cm.

C. 6 cm.

D. 7 cm.

Phương pháp giải:

Áp dụng định lí Thalès với các cặp đường thẳng song song EF và CD, DE và BC.

Lời giải chi tiết:

Áp dụng định lí Thalès:

• Với DE // BC (E ∈ AC) ta có: \(\frac{{A{\rm{D}}}}{{AB}} = \frac{{A{\rm{E}}}}{{AC}} = \frac{9}{{12}} = \frac{2}{3}\)

• Với EF // CD (F ∈ AB) ta có: \(\frac{{AF}}{{A{\rm{D}}}} = \frac{{A{\rm{E}}}}{{AC}} = \frac{2}{3}\)

Suy ra: \(AF = \frac{2}{3}AD = \frac{2}{3}.6 = 4(cm)\)

Vậy AF = 4 cm.

=> Chọn đáp án A.