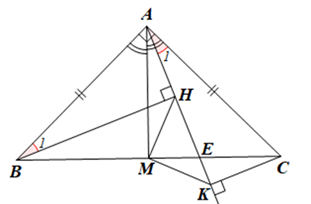
Giải Bài 91 trang 95 sách bài tập toán 7 - Cánh diềuCho tam giác ABC vuông cân ở A có đường phân giác AM. Gọi E là điểm nằm giữa B và C. Vẽ BH và CK vuông góc với AE (H, K thuộc AE). Tổng hợp đề thi học kì 1 lớp 7 tất cả các môn - Cánh diều Toán - Văn - Anh - Khoa học tự nhiên... Đề bài Cho tam giác ABC vuông cân ở A có đường phân giác AM. Gọi E là điểm nằm giữa B và C. Vẽ BH và CK vuông góc với AE (H, K thuộc AE). a) Chứng minh ba đường trung trực tương ứng của các đoạn thẳng AB, AC, KH cùng đi qua điểm M. b) Tính số đo các góc của tam giác MKH. Phương pháp giải - Xem chi tiết - Chứng minh: M nằm trên đường trung trực của AB và AC và M nằm trên đường trung trực của HK nên ba đường trung trực tương ứng của các đoạn thẳng AB, AC, KH cùng đi qua điểm M. - Sử dụng tổng ba góc trong một tam giác, hai tam giác bằng nhau và tam giác cân để tính số đo các góc của tam giác MKH. Lời giải chi tiết
a) • Xét ∆ABM và ∆ACM có: AB = AC (do ∆ABC cân tại A), \(\widehat {BAM} = \widehat {CAM}\) (do AM là tia phân giác của góc BAC), AM là cạnh chung Do đó ∆ABM = ∆ACM (c.g.c) Suy ra MB = MC (hai cạnh tương ứng). • Ta có AM là tia phân giác của góc BAC nên: \(\widehat {BAM} = \widehat {CAM} = \frac{1}{2}\widehat {BAC} = \frac{1}{2}.90^\circ = 45^\circ \) Lại có \(\widehat {ABC} + \widehat {ACB} + \widehat {BAC} = 180^\circ \) (tổng ba góc trong tam giác ABC) Mà \(\widehat {BAC} = 90^\circ \) và \(\widehat {ABC} = \widehat {ACB}\) (do ∆ABC cân tại A) Nên \(\widehat {ABC} = \widehat {ACB} = \frac{{180^\circ - \widehat {BAC}}}{2} = \frac{{180^\circ - 90^\circ }}{2} = 45^\circ \) Xét ∆ABM có \(\widehat {MBA} = \widehat {MAB}\) (cùng bằng 45°) nên tam giác ABM cân tại M. Suy ra MA = MB Mà MB = MC nên MA = MB = MC. Do đó M nằm trên đường trung trực của AB và AC (1) •Trong tam giác ABH vuông tại H có \({\hat B_1} + \widehat {BAH} = 90^\circ \) (trong tam giác vuông, tổng hai góc nhọn bằng 90°) Nên \({\hat B_1} = 90^\circ - \widehat {BAH}\) Mà \({\hat A_1} = \widehat {BAC} - \widehat {BAH} = 90^\circ - \widehat {BAH}\) Suy ra \({\hat B_1} = {\hat A_1}\) Xét ∆BAH và ∆ACK có: \(\widehat {BHA} = \widehat {AKC}\left( { = 90^\circ } \right)\) \({\hat B_1} = {\hat A_1}\) (chứng minh trên), AB = AC (chứng minh ở câu a), Do đó ∆ABH = ∆CAK (cạnh huyển – góc nhọn). Suy ra AH = CK (hai cạnh tương ứng) và \(\widehat {BAH} = \widehat {ACK}\) (hai góc tương ứng). Ta có \(\widehat {BAH} = \widehat {BAM} + \widehat {MAH} = 45^\circ + \widehat {MAH}\) Mà \(\widehat {BAH} = \widehat {ACK}\) (chứng minh trên) Suy ra \(\widehat {MAH} = \widehat {MCK}\). Xét ∆AMH và ∆CMK có: AH = CK (chứng minh trên), \(\widehat {MAH} = \widehat {MCK}\) (chứng minh trên), AM = AM (chứng minh ở câu a) Do đó ∆AMH = ∆CMK (c.g.c) Suy ra MH = MK (hai cạnh tương ứng) Hay M nằm trên đường trung trực của HK (2) Từ (1) và (2) ta có điểm M nằm trên đường trung trực của AB, AC, HK. Vậy ba đường trung trực tương ứng của các đoạn thẳng AB, AC, KH cùng đi qua điểm M. b) • Ta có \(\widehat {AMH} = \widehat {CMK}\) (hai góc tương ứng của ∆AMH = ∆CMK). Mà \(\widehat {HMK} = \widehat {HMC} + \widehat {CMK}\) Do đó\(\widehat {HMK} = \widehat {HMC} + \widehat {AMH} = \widehat {AMC} = 90^\circ \) nên tam giác MHK vuông tại H. • Ta có MH = MK nên tam giác MHK cân tại M. Suy ra \(\widehat {MHK} = \widehat {MKH}\) •Trong tam giác MHK vuông tại H có \(\widehat {MHK} + \widehat {MKH} = 90^\circ \) (trong tam giác vuông, tổng hai góc nhọn bằng 90°). Mà \(\widehat {MHK} = \widehat {MKH}\) (chứng minh trên) Suy ra\(\widehat {MHK} = \widehat {MKH} = \frac{{90^\circ }}{2} = 45^\circ \) Vậy ∆MKH có \(\widehat {MHK} = \widehat {MKH} = 45^\circ ,\widehat {HMK} = 90^\circ \)
|