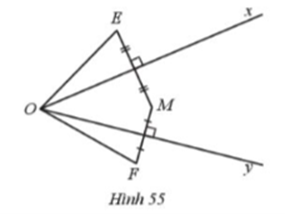
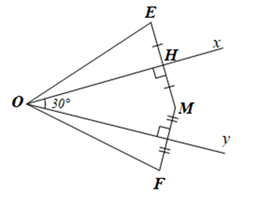
Giải Bài 89 trang 94 sách bài tập toán 7 - Cánh diềuCho góc nhọn xOy và điểm M nằm trong góc xOy. Gọi E, F là hai điểm nằm ngoài góc xOy sao cho Ox là đường trung trực của đoạn thẳng ME, Oy là đường trung trực của đoạn thẳng MF (Hình 55). Đề bài Cho góc nhọn xOy và điểm M nằm trong góc xOy. Gọi E, F là hai điểm nằm ngoài góc xOy sao cho Ox là đường trung trực của đoạn thẳng ME, Oy là đường trung trực của đoạn thẳng MF (Hình 55). Chứng minh: a) O là giao điểm ba đường trung trực của tam giácEMF. b) Nếu \(\widehat {xOy} = 30^\circ \) thì \(\widehat {EOF} = 60^\circ \). Phương pháp giải - Xem chi tiết - Gọi O là giao điểm hai đường trung trực của ME và MF chứng minh O là giao điểm ba đường trung trực của tam giác EMF. - Cho \(\widehat {xOy} = 30^\circ \) chứng minh: \(\widehat {EOM} = 2\widehat {xOM}\) và \(\widehat {MOF} = 2\widehat {MOy}\) từ đó chứng minh \(\widehat {EOF} = \widehat {EOM} + \widehat {MOF} = 2\widehat {xOM} + 2\widehat {MOy}\)\( = 2\left( {\widehat {xOM} + \widehat {MOy}} \right) = 2\widehat {xOy} = 2.30^\circ = 60^\circ \) Lời giải chi tiết a) Trong tam giác EMF có O là giao điểm hai đường trung trực của ME và MF nên O là giao điểm ba đường trung trực của tam giác EMF. Vậy O là giao điểm ba đường trung trực của tam giác FEM. b) Gọi H là trung điểm của EM. Xét ∆OEH và ∆OMH có: \(\widehat {OHE} = \widehat {OHM}\left( { = 90^\circ } \right)\) OH là cạnh chung, EH = MH (do H là trung điểm của EM). Do đó ∆OEH = ∆OMH (hai cạnh góc vuông). Suy ra \(\widehat {{\rm{EOH}}} = \widehat {MOH}\) (hai góc tương ứng). Do đó Ox là tia phân giác của góc EOM nên \(\widehat {{\rm{EOx}}} = \widehat {xOM} = \frac{1}{2}\widehat {{\rm{EOM}}}\) Hay \(\widehat {EOM} = 2\widehat {xOM}\). Chứng minh tương tự ta cũng có: \(\widehat {{\rm{FOy}}} = \widehat {MOy} = \frac{1}{2}\widehat {{\rm{MOF}}}\) Hay\(\widehat {MOF} = 2\widehat {MOy}\)
Vậy nếu \(\widehat {xOy} = 30^\circ \) thì \(\widehat {EOF} = 60^\circ \).
|