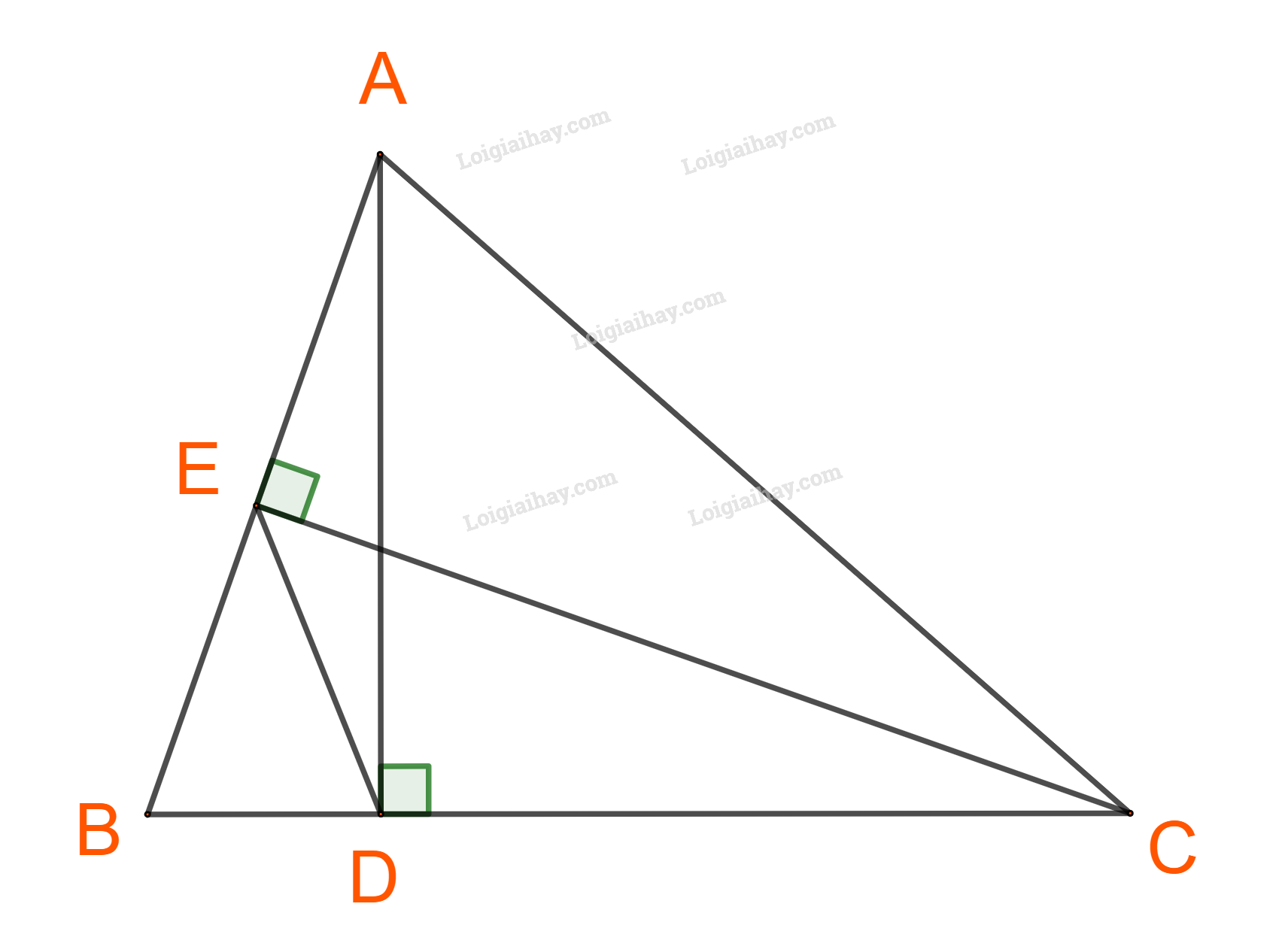
Giải bài 9 trang 73 SGK Toán 10 tập 1 – Chân trời sáng tạo

Đề bài

Cho tam giác ABC có góc B nhọn, AD và CE là hai đường cao.

a) Chứng minh $\frac{{{S_{BDE}}}}{{{S_{BAC}}}} = \frac{{BD.BE}}{{BA.BC}}.$

b) Biết rằng ${S_{ABC}} = 9{S_{BDE}}$ và $DE = 2\sqrt 2 .$ Tính $\cos B$ và bán kính đường tròn ngoại tiếp tam giác ABC.

Lời giải chi tiết

 

a) Áp dụng công thức $S = \frac{1}{2}ac.\sin B$ cho tam giác ABC và BED, ta có:

${S_{ABC}} = \frac{1}{2}.BA.BC.\sin B;{S_{BED}} = \frac{1}{2}..BE.BD.\sin B$

$\Rightarrow \frac{{{S_{BED}}}}{{{S_{ABC}}}} = \frac{{\frac{1}{2}.BE.BD.\sin B}}{{\frac{1}{2}.BA.BC.\sin B}} = \frac{{BE.BD}}{{BA.BC}}$

b) Ta có: $\cos B = \frac{{BD}}{{BA}} = \frac{{BE}}{{BC}}$

Mà $\frac{{{S_{BED}}}}{{{S_{ABC}}}} = \frac{1}{9} \Rightarrow \frac{{BD}}{{BA}}.\frac{{BE}}{{BC}} = \frac{1}{9}$

$\Rightarrow \cos B = \frac{{BD}}{{BA}} = \frac{{BE}}{{BC}} = \frac{1}{3}$

+) Xét tam giác ABC và tam giác DEB ta có:

$\frac{{BE}}{{BC}} = \frac{{BD}}{{BA}} = \frac{1}{3}$ và góc B chung

$\Rightarrow \Delta ABC \sim \Delta DEB$ (cgc)

$\Rightarrow \frac{{DE}}{{AC}} = \frac{1}{3} \Rightarrow AC = 3.DE = 3.2\sqrt 2  = 6\sqrt 2 .$

Ta có: $\cos B = \frac{1}{3} \Rightarrow \sin B = \sqrt {1 - {{\left( {\frac{1}{3}} \right)}^2}}  = \frac{{2\sqrt 2 }}{3}$ (do B là góc nhọn)

Áp dụng định lí sin trong tam giác ABC ta có:

$\frac{{AC}}{{\sin B}} = 2R \Rightarrow R = \frac{{6\sqrt 2 }}{{\frac{{2\sqrt 2 }}{3}}}:2 = \frac{9}{2}$