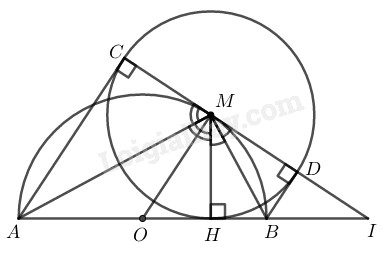
Bài 88 trang 172 SBT toán 9 tập 1Giải bài 88 trang 172 sách bài tập toán 9. Cho nửa đường tròn tâm O có đường kính AB. Gọi M là điểm bất kì thuộc nửa đường tròn, H là chân đường vuông góc kẻ từ M đến AB. Vẽ đường tròn (M ; MH). Kẻ các tiếp tuyến AC, BD với đường tròn tâm M ( C và D là các tiếp điểm khác H)... Đề bài Cho nửa đường tròn tâm \(O\) có đường kính \(AB.\) Gọi \(M\) là điểm bất kì thuộc nửa đường tròn, \(H\) là chân đường vuông góc kẻ từ \(M\) đến \(AB.\) Vẽ đường tròn \((M ; MH).\) Kẻ các tiếp tuyến \(AC, BD\) với đường tròn tâm \(M ( C\) và \(D\) là các tiếp điểm khác \(H).\) \(a)\) Chứng minh rằng ba điểm \(C, M, D\) thẳng hàng và \(CD\) là tiếp tuyến của đường tròn \((O).\) \(b)\) Chứng minh rằng khi điểm \(M\) di chuyển trên nửa đường tròn \((O)\) thì tổng \(AC + BD\) không đổi. \(c)\) Giả sử \(CD\) và \(AB\) cắt nhau tại \(I.\) Chứng minh rằng tích \(OH.OI\) không đổi. Phương pháp giải - Xem chi tiết Sử dụng kiến thức: \(*\)) Nếu hai tiếp tuyến của một đường tròn cắt nhau tại một điểm thì +) Điểm đó cách đều hai tiếp điểm. +) Tia kẻ từ tâm đi qua điểm đó là tia phân giác của góc tạo bởi hai bán kính đi qua các tiếp điểm. \(*\)) Nếu một đường thẳng là tiếp tuyến của một đường tròn thì nó vuông góc với bán kính đi qua tiếp điểm. \(*\)) Đường trung bình của hình thang thì song song với hai cạnh đáy và bằng nửa tổng hai đáy. \(*\)) Hệ thức lượng trong tam giác vuông: Bình phương cạnh góc vuông bằng tích cạnh huyền với hình chiếu cạnh góc vuông đó trên cạnh huyền. Lời giải chi tiết
\(a)\) Trong đường tròn \((M; MH),\) có AC và AH là 2 tiếp tuyến cắt nhau tại A, theo tính chất hai tiếp tuyến cắt nhau, ta có: \( MA\) là tia phân giác của góc \(HMC\) và \(AC=AH\) Suy ra: \(\widehat {CMA} = \widehat {HMA}\) hay \(\widehat {CMH} = 2\widehat {HMA}\) Trong đường tròn \((M; MH),\) có BD và BH là 2 tiếp tuyến cắt nhau tại B, theo tính chất hai tiếp tuyến cắt nhau, ta có: \(MB\) là tia phân giác của góc \(HMD\) và \(BD=BH\) Suy ra: \(\widehat {HMB} = \widehat {DMB}\) hay \(\widehat {DMH} = 2\widehat {HMB}\) Tam giác \(ABM\) nội tiếp đường tròn \((O)\) có \(AB\) là đường kính nên vuông tại \(M\) Suy ra: \(\widehat {AMB} = 90^\circ \) hay \(\widehat {HMA} + \widehat {HMB} = 90^\circ \) Suy ra: \(\widehat {CMH} + \widehat {HMD} = 2\widehat {HMA} + 2\widehat {HMB}\) \(= 2 (\widehat {HMA} + \widehat {HMB}) = 2.90^\circ = 180^\circ \) Vậy \(C, M, D\) thẳng hàng. \(b)\) Theo câu a) ta có: \(AC = AH\) và \(BD = BH\) Khi \(M\) thay đổi trên nửa đường tròn tâm \(O\) thì \(AC\) luôn bằng \(AH\) và \(BD\) luôn bằng \(BH.\) Suy ra: \(AC + BD = AH + BH = AB\) không đổi \(c)\) Ta có: \(AC ⊥ CD \) và \( BD ⊥ CD\) ( tính chất tiếp tuyến) Suy ra: \(AC // BD\) hay tứ giác \(ABDC\) là hình thang Mà \(OA = OB \) (= bán kính \((O)\)) Và \(MC = MD\) (= bán kính \((M)\)) Suy ra \(OM\) là đường trung bình của hình thang \(ABCD\) Khi đó \(OM // AC.\) Suy ra: \(OM ⊥ CD\) hay \(\widehat {OMI} = 90^\circ \) Tam giác \(OMI\) vuông tại \(M\) có \(MH ⊥ OI.\) Theo hệ thức lượng trong tam giác vuông, ta có: \(OM^2= OH.OI\) Mà OM là bán kính đường tròn (O) nên OM có độ dài không đổi. Suy ra: \(OH.OI \) không đổi. HocTot.Nam.Name.Vn  Chia sẻ Bình luận
Tham Gia Group 2K10 Ôn Thi Vào Lớp 10 Miễn Phí
|
