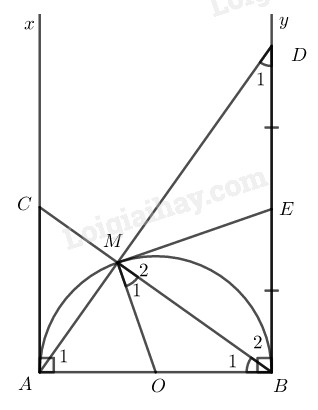
Bài 2.2 phần bài tập bổ sung trang 173 SBT toán 9 tập 1

Đề bài

Cho nửa đường tròn $(O)$ đường kính $AB.$ Trên nửa mặt phẳng bờ $AB$ chứa nửa đường tròn, vẽ các tia tiếp tuyến $Ax$ và $By$ với nửa đường tròn. Gọi $M$ là điểm thuộc nửa đường tròn, $D$ là giao điểm của $AM$ và $By,$ $C$ là giao điểm của $BM$ và $Ax,$ $E$ là trung điểm của BD. Chứng minh rằng:

$a)$ $AC.BD = AB^2;$

$b)$ $ME$ là tiếp tuyến của nửa đường tròn.

Lời giải chi tiết

$a)$ Xét tam giác ABD vuông tại B có $\widehat {{A_1}} + \widehat {{D_1}}=90^0$ (1)

Tam giác AMB nội tiếp đường tròn (O) có AB là đường kính nên vuông tại M.

Suy ra $\widehat {{A_1}} + \widehat {{B_1}}=90^0$ (2)

Từ (1) và (2) suy ra: $\widehat {{B_1}} = \widehat {{D_1}}$ ( cùng phụ với $\widehat {{A_1}}$).

Xét $∆ABC$ và $∆BDA$ có:

$\widehat {{B_1}} = \widehat {{D_1}}$ (cmt)

$\widehat A = \widehat B = 90^\circ$

Suy ra $∆ABC$ đồng dạng với $∆BDA \;\;(g.g)$ suy ra:

$\displaystyle{{AB} \over {BD}} = {{AC} \over {BA}}$(cặp cạnh tương ứng tỉ lệ), do đó $AC . BD = AB^2$

$b)$ Vì tam giác AMB vuông tại M (cmt) nên $AD\bot BM$ 

Suy ra tam giác BMD vuông tại M.

Ta có $∆MBD$ vuông tại M có ME là đường trung tuyến nên $ED = EM = EB$

 Suy ra $∆EBM$ cân tại E nên $\widehat {{M_2}} = \widehat {{B_2}}$$(1)$

Lại có $∆MOB$ cân tại $O$ (do $OM=OB)$ nên $\widehat {{M_1}} = \widehat {{B_1}}$ $(2)$

Từ $(1)$ và $(2)$ suy ra

$\widehat {{M_1}} + \widehat {{M_2}}$ = $\widehat {{B_1}} + \widehat {{B_2}}$ $=\widehat {{OBD}}=90^\circ$

Hay $\widehat {{OME}}=90^0$ tức là $ME ⊥ OM$ tại $M.$

Vậy $ME$ là tiếp tuyến của nửa đường tròn (O).

HocTot.Nam.Name.Vn