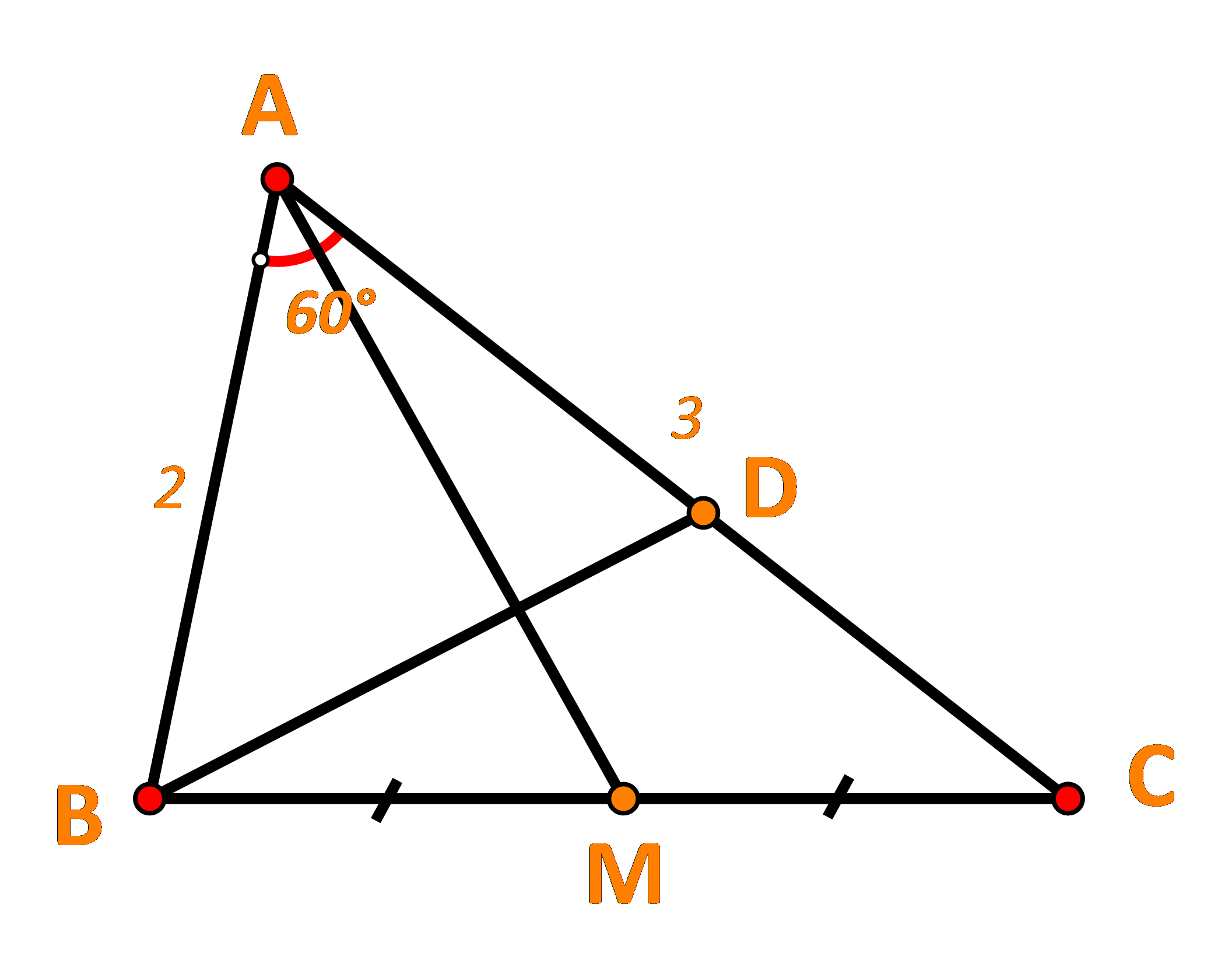
Giải bài 8 trang 98 SGK Toán 10 tập 1 – Cánh diềuCho tam giác ABC có AB = 2,AC = 3,BAC = 60 Gọi M là trung điểm của đoạn thẳng BC. Tổng hợp đề thi học kì 2 lớp 10 tất cả các môn - Cánh diều Toán - Văn - Anh - Lí - Hóa - Sinh - Sử - Địa... Đề bài Cho tam giác ABC có AB=2,AC=3,^BAC=60o. Gọi M là trung điểm của đoạn thẳng BC. Điểm D thỏa mãn →AD=712→AC. a) Tính →AB.→AC b) Biểu diễn →AM,→BD theo →AB,→AC c) Chứng minh AM⊥BD. Phương pháp giải - Xem chi tiết +) Tính →AB.→AC bằng công thức →AB.→AC=|→AB|.|→AC|.cos(→AB,→AC)=AB.AC.cos^BAC +) M là trung điểm BC ⇔→AB+→AC=2→AM với điểm A bất kì. +) AM⊥BD⇔→AM.→BD=0 Lời giải chi tiết
a) →AB.→AC=2.3.cos^BAC=6.cos60o=3 b) Ta có: →AB+→AC=2→AM(do M là trung điểm của BC) ⇔→AM=12→AB+12→AC +) →BD=→AD−→AB=712→AC−→AB c) Ta có: →AM.→BD=(12→AB+12→AC)(712→AC−→AB)=724→AB.→AC−12→AB2+724→AC2−12→AC.→AB=−12AB2+724AC2−524→AB.→AC=−12.22+724.32−524.3=0 ⇒AM⊥BD
>> 2K9 Học trực tuyến - Định hướng luyện thi TN THPT, ĐGNL, ĐGTD ngay từ lớp 11 (Click để xem ngay) cùng thầy cô giáo giỏi trên Tuyensinh247.com. Bứt phá điểm 9,10 chỉ sau 3 tháng, tiếp cận sớm các kì thi.
|