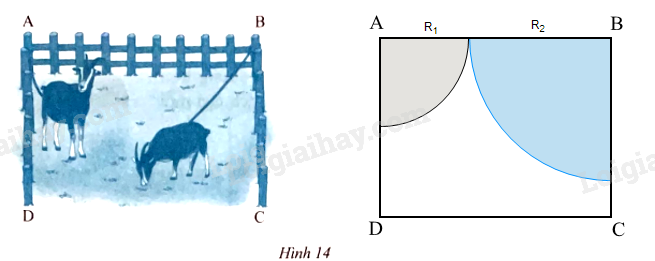
Giải bài 8 trang 98 sách bài tập toán 9 - Chân trời sáng tạo tập 1Một vườn cỏ có dạng hình chữ nhật ABCD với AB = 40 m, AD = 30 m. Người ta muốn buộc hai con dê ở hai góc vườn A, B. Có hai cách buộc: Cách 1: Mỗi dây thừng dài 20 m. Cách 2: Một dây thừng dài 30 m và một dây thừng dài 10 m. Hỏi với cách buộc nào thì diện tích cỏ mà hai con dê có thể ăn được sẽ lớn hơn? Đề bài Một vườn cỏ có dạng hình chữ nhật ABCD với AB = 40 m, AD = 30 m. Người ta muốn buộc hai con dê ở hai góc vườn A, B. Có hai cách buộc: Cách 1: Mỗi dây thừng dài 20 m. Cách 2: Một dây thừng dài 30 m và một dây thừng dài 10 m. Hỏi với cách buộc nào thì diện tích cỏ mà hai con dê có thể ăn được sẽ lớn hơn?
Phương pháp giải - Xem chi tiết Dựa vào: Diện tích hình quạt tròn: S=πR2n360. Lời giải chi tiết Diện tích cỏ hai con dê có thể ăn là dạng hai hình quạt có số đo cung cùng bằng 90o. TH1: Mỗi dây thừng dài 20 m suy ra R1 = R2 = 20 m. Diện tích cỏ mà hai con dê có thể ăn: S=S1+S2=πR21.90360+πR22.90360=π.202.90360+π.202.90360=200π(m2) TH2: Giả sử dây thừng cột con dê ở A dài 30 m, dây thừng cột con dê ở B dài 10 m. Suy ra R1 = 30 m, R2 = 10 m. Diện tích cỏ mà hai con dê có thể ăn: S=S1+S2=πR21.90360+πR22.90360=π.302.90360+π.102.90360=250π(m2). Vậy dùng hai sợi dây 30 m và 10 m thì diện tích cỏ hai con dê sẽ ăn nhiều hơn.
>> Học trực tuyến Lớp 9 & Lộ trình UP10 trên Tuyensinh247.com >> Chi tiết khoá học xem: TẠI ĐÂY Đầy đủ khoá học các bộ sách (Kết nối tri thức với cuộc sống; Chân trời sáng tạo; Cánh diều), theo lộ trình 3: Nền Tảng, Luyện Thi, Luyện Đề. Bứt phá điểm lớp 9, thi vào lớp 10 kết quả cao. Hoàn trả học phí nếu học không hiệu quả.
|