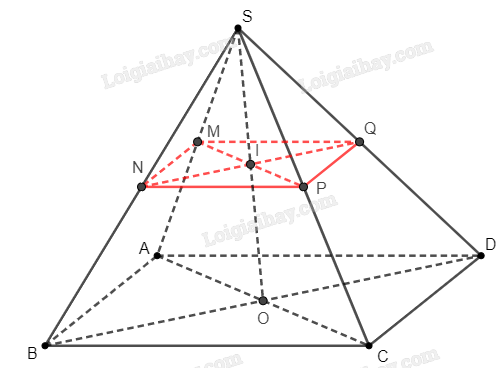
Giải bài 8 trang 95 sách bài tập toán 11 - Cánh diềuCho hình chóp \(S.ABCD\) có đáy là hình bình hành. Gọi \(M,{\rm{ }}N,{\rm{ }}P\) lần lượt là trung điểm của các cạnh \(SA,{\rm{ }}SB,{\rm{ }}SC\). Đề bài Cho hình chóp \(S.ABCD\) có đáy là hình bình hành. Gọi \(M,{\rm{ }}N,{\rm{ }}P\) lần lượt là trung điểm của các cạnh \(SA,{\rm{ }}SB,{\rm{ }}SC\). a) Xác định giao điểm \(I\) của đường thẳng \(MP\) với mặt phẳng \(\left( {SBD} \right)\). b) Xác định giao điểm \(Q\) của đường thẳng \(SD\) với mặt phẳng \(\left( {MNP} \right)\). Phương pháp giải - Xem chi tiết Để xác định giao điểm của mặt phẳng với một đường thẳng cho trước, ta cần chọn một đường thẳng khác nằm trong mặt phẳng đã cho, rồi tìm giao điểm của 2 đường thẳng đó. Lời giải chi tiết a) Trên mặt phẳng \(\left( {ABCD} \right)\), gọi \(\left\{ O \right\} = AC \cap BD\). Trên mặt phẳng \(\left( {SAC} \right)\), gọi \(\left\{ I \right\} = MP \cap SO\). Do \(SO \subset \left( {SBD} \right)\), ta suy ra \(\left\{ I \right\} = MP \cap \left( {SBD} \right)\). Vậy \(I\) là giao điểm của \(MP\) và \(\left( {SBD} \right)\).
b) Trên mặt phẳng \(\left( {SBD} \right)\), gọi \(\left\{ Q \right\} = NI \cap SD\). Do \(NI \subset \left( {MNP} \right)\), ta suy ra \(\left\{ Q \right\} = \left( {MNP} \right) \cap SD\). Vậy \(Q\) là giao điểm của \(SD\) và \(\left( {MNP} \right)\).  Chia sẻ Bình luận
Tham Gia Group Dành Cho 2K8 Chia Sẻ, Trao Đổi Tài Liệu Miễn Phí
|
