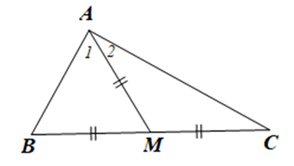
Giải Bài 75 trang 90 sách bài tập toán 7 - Cánh diều

Đề bài

 Tam giác ABC có đường trung tuyến AM bằng nửa cạnh BC. Chứng minh rằng $\widehat {BAC} = 90^\circ$

Lời giải chi tiết

 

Ta có: $AM = \frac{1}{2}BC, BM = MC$ nên $AM = BM = MC$.

Suy ra hai tam giác AMB và AMC cân tại M.

Do đó $\widehat B = {\hat A_1},\hat C = {\hat A_2}$

Xét $\Delta ABC$ có $\widehat B + \widehat C + \widehat {BAC} = 180^\circ$ (tổng ba góc của một tam giác)

Suy ra ${\widehat A_1} + {\widehat A_2} + \widehat {BAC} = 180^\circ$ hay $\widehat {BAC} + \widehat {BAC} = 180^\circ$

Nên $2\widehat {BAC}= 180^\circ$

Do đó $\widehat {BAC} = \frac{{180^\circ }}{2} = 90^\circ$

Vậy $\widehat {BAC} = 90^\circ$