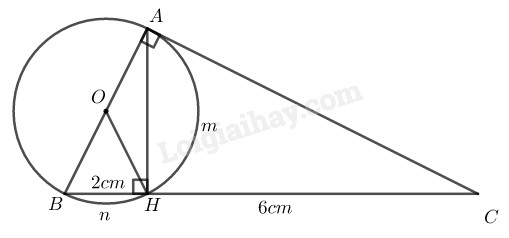
Bài 72 trang 113 SBT toán 9 tập 2

Đề bài

Cho tam giác $ABC$ vuông ở $A$ và đường cao $AH.$ Vẽ đường tròn tâm $O$ đường kính $AB.$ Biết $BH = 2cm$ và $HC = 6cm.$ Tính:

$a)$ Diện tích hình tròn $(O).$

$b)$ Tổng diện tích hai hình viên phân $AmH$ và $BnH$ (ứng với các cung nhỏ).

$c)$ Diện tích hình quạt tròn $AOH$ (ứng với cung nhỏ $AH$).

Lời giải chi tiết

$a)$ $∆ABC$ có $\widehat A = {90^0}$

Theo hệ thức lượng trong tam giác vuông ta có:

$A{B^2} = BH.BC$$\Rightarrow A{B^2} = 2.\left( {2 + 6} \right) = 16$

Suy ra $AB = 4\, (cm)$

Diện tích hình tròn tâm $O$ là:

$S = \displaystyle \pi {\left( {{{AB} \over 2}} \right)^2}$$= \displaystyle \pi {\left( {{4 \over 2}} \right)^2} = 4\pi$ $(cm^2)$

$b)$ Trong tam giác vuông $ABC$ ta có:

$A{H^2} = HB.HC = 2.6 = 12$

Suy ra $AH = 2\sqrt 3$ $(cm)$

$S_{\Delta AHB}= \displaystyle {1 \over 2}AH.BH$$= \displaystyle {1 \over 2}.2.2\sqrt 3  = 2\sqrt 3$ $(cm^2)$

Tổng diện  tích hai hình viên phân $AmH$ và $BnH$ bằng diện tích nửa hình tròn tâm $O$ trừ diện tích $∆AHB$ nên tổng diện tích hai hình viên phân là:

$S = 2\pi  - 2\sqrt 3  = 2\left( {\pi  - \sqrt 3 } \right)$ $(cm^2)$

$c)$ $∆BOH$ có $OB = OH = BH = 2 cm$

$\Rightarrow \Delta BOH$ đều

$\Rightarrow \widehat B = {60^0}$

$\widehat B = \displaystyle {1 \over 2} sđ \overparen{AmH}$ (tính chất góc nội tiếp)

$\Rightarrow  sđ \overparen{AmH}$ $= 2\widehat B = {120^0}$

$S_{qAOH}=\displaystyle {{\pi {{.2}^2}.120} \over {360}} = \displaystyle {{4\pi } \over 3}$  $(cm^2)$

HocTot.Nam.Name.Vn