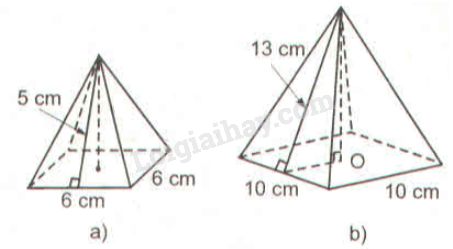
Bài 70 trang 153 SBT toán 8 tập 2Giải bài trang sách bài tập toán 8. Tính thể tích và diện tích toàn phần các hình chóp đều dưới đây (theo các kích thước cho trên hình vẽ 153). Đề bài Tính thể tích và diện tích toàn phần các hình chóp đều dưới đây (theo các kích thước cho trên hình vẽ 153).
Phương pháp giải - Xem chi tiết Sử dụng: - Thể tích của hình chóp đều bằng một phần ba diện tích mặt đáy nhân với chiều cao. \(V = \dfrac{1}{3} .S.h\) Trong đó: \(S\) là diện tích đáy, \(h\) là chiều cao. - Định lí Pytago trong tam giác vuông: Bình phương của cạnh huyền bằng tổng các bình phương của các cạnh góc vuông. - Diện tích xung quanh của hình chóp đều bằng tích của nửa chu vi đáy với trung đoạn. \({S_{xq}} = pd\) Trong đó: \(p\) là nửa chu vi đáy, \(d\) là trung đoạn của hình chóp đều. - Diện tích toàn phần bằng tổng của diện tích xung quanh và diện tích đáy hình chóp. Lời giải chi tiết - Hình a: Đường cao hình chóp bằng: \(h=\sqrt {{5^2} - {3^2}} = \sqrt {25 - 9} = \sqrt {16} \)\(\,= 4\,(cm)\) Diện tích đáy bằng: \(S = 6.6 = 36\;(c{m^2})\) Thể tích hình chóp bằng: \(\displaystyle V = {1 \over 3}S.h = {1 \over 3}.36.4 = 48(c{m^3})\) Diện tích xung quanh bằng: \({S_{xq}} = pd = 2.6.5 = 60\;(c{m^2})\) Diện tích toàn phần là: \({S_{TP}} = {S_{xq}} + {S_đ}= 60 + 36 \)\(\,= 96\;(c{m^2})\) - Hình b: Đường cao hình chóp bằng: \(h=\sqrt {{{13}^2} - {5^2}} = \sqrt {144} = 12\,(cm)\) Diện tích đáy của hình chóp bằng: \(S = 10.10 = 100\;(c{m^2})\) Thể tích hình chóp bằng: \(\displaystyle V = {1 \over 3}S.h = {1 \over 3}.100.12 = 400\,(c{m^3})\) Diện tích xung quanh hình chóp bằng: \({S_{xq}} = pd = 10.2.13 = 260\;(c{m^2})\) Diện tích toàn phần của hình chóp bằng: \({S_{TP}} = {S_{xq}} + {S_đ}= 260 + 100 \)\(\,= 360 \;(c{m^2})\). HocTot.Nam.Name.Vn  Chia sẻ Bình luận
Tham Gia Group Dành Cho 2K11 Chia Sẻ, Trao Đổi Tài Liệu Miễn Phí
|
