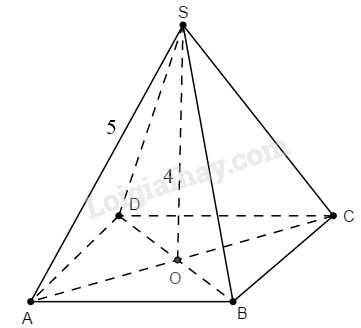
Bài 68 trang 152 SBT toán 8 tập 2

Đề bài

Hình chóp tứ giác đều có độ dài cạnh bên là \(5cm\), chiều cao hình chóp là \(4cm.\) Thể tích của hình chóp là:

A. \(30\;c{m^3}\)                          B. \(24\;c{m^3}\)

C. \(22\;c{m^3}\)                          D. \(18\;c{m^3}\)

E. \(15\;c{m^3}\)

Hãy chọn kết quả đúng.

Lời giải chi tiết

Giả sử hình chóp tứ giác đều \(S.ABCD\) có độ dài cạnh bên là \(SA=5cm\), chiều cao \(SO=4cm.\)

Áp dụng định lí Py-ta-go vào tam giác vuông \(SOA\), ta có:

\(S{A^2} = S{O^2} + O{A^2}\)

\(\Rightarrow OA = \sqrt {S{A^2} - S{O^2}} \)

\( \Rightarrow OA = \sqrt {{5^2} - {4^2}}  = 3\,\left( {cm} \right)\)

\( \Rightarrow  AC=BD =2OA=2.3= 6\;(cm).\)

Diện tích đáy \(ABCD\) là: \(S=\displaystyle{1 \over 2}.AC.BD= \displaystyle{1 \over 2}.6.6 = 18\;(c{m^2})\)

Thể tích hình chóp đều \(S.ABCD\) là:

\(\displaystyle V = \displaystyle {1 \over 3}S.h = {1 \over 3}.18.4 = 24\;(c{m^3})\)

Chọn B.

HocTot.Nam.Name.Vn