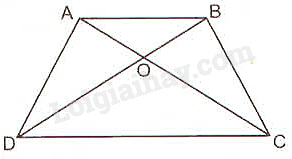
Giải bài 7 trang 51 SGK Toán 8 tập 2– Chân trời sáng tạoCho hình thang Đề bài Cho hình thang \(ABCD\left( {AB//CD} \right)\) có hai đường chéo \(AC\) và \(BD\) cắt nhau tại \(O\). Chứng minh rằng \(OA.OD = OB.OC\) Video hướng dẫn giải Phương pháp giải - Xem chi tiết Sử dụng hệ quả của định lí Thales. Nếu một đường thẳng cắt hai cạnh của một tam giác và song song với cạnh thứ ba thì tạo ra một tam giác mới có ba cạnh tương ứng tỉ lệ với ba cạnh của tam giác đã cho. Lời giải chi tiết
Xét tam giác \(OCD\) có \(AB//CD\) (giả thiết) và \(AB\) cắt \(OC;OD\) lần lượt tại \(A;B\). Theo hệ quả của định lí Thales ta có: \(\frac{{OA}}{{OC}} = \frac{{OB}}{{OD}} = \frac{{AB}}{{CD}} \Rightarrow \frac{{OA}}{{OC}} = \frac{{OB}}{{OD}} \Rightarrow OA.OD = OB.OC\) (điều phải chứng minh).  Chia sẻ Bình luận
Tham Gia Group Dành Cho 2K11 Chia Sẻ, Trao Đổi Tài Liệu Miễn Phí
|
