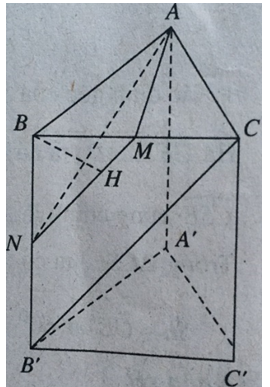
Bài 7 trang 200 SBT hình học 11Giải bài 7 trang 200 sách bài tập hình học 11. Cho lăng trụ đứng ABC.A'B'C' có đáy ABC là tam giác vuông với AB = BC = a, cạnh bên AA' = a√2. Gọi M là trung điểm BC. Tính khoảng cách giữa hai đường thẳng AM, B'C. Đề bài Cho lăng trụ đứng ABC.A'B'C' có đáy ABC là tam giác vuông với AB = BC = a, cạnh bên AA' = a√2. Gọi M là trung điểm BC. Tính khoảng cách giữa hai đường thẳng AM, B'C. Lời giải chi tiết
Gọi N là trung điểm của BB’, ta có: CB’ // MN nên CB’ // (AMN). Như vậy d(BC’, AM) = d(B’, (AMN)) = d(B, (AMN)) (vì B, B’ đối xứng qua N ∈ (AMN)). Hạ BH ⊥ (AMN), ta có d(B, (AMN)) = BH. Nhận xét: Tứ diện B.AMN có ba cạnh BA, BM, BN vuông góc nhau từng đôi một nên \(\dfrac{1}{{B{H^2}}} = \dfrac{1}{{B{A^2}}} + \dfrac{1}{{B{M^2}}} + \dfrac{1}{{B{N^2}}} = \dfrac{7}{{{a^2}}}\) \( \Rightarrow BH = \dfrac{{a\sqrt 7 }}{7}\) HocTot.Nam.Name.Vn
>> 2K8 Chú ý! Lộ Trình Sun 2026 - 3IN1 - 1 lộ trình ôn 3 kì thi (Luyện thi 26+TN THPT, 90+ ĐGNL HN, 900+ ĐGNL HCM; 70+ ĐGTD - Click xem ngay) tại Tuyensinh247.com.Đầy đủ theo 3 đầu sách, Thầy Cô giáo giỏi, 3 bước chi tiết: Nền tảng lớp 12; Luyện thi chuyên sâu; Luyện đề đủ dạng đáp ứng mọi kì thi.
|