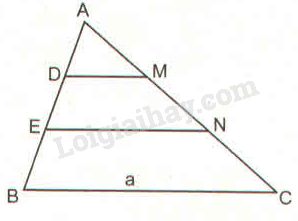
Bài 6 trang 84 SBT toán 8 tập 2

Đề bài

Cho tam giác $ABC$ có cạnh $BC = a.$ Trên cạnh $AB$ lấy các điểm $D$ và $E$ sao cho $AD = DE = EB.$ Từ $D, E$ kẻ các đường thẳng song song với $BC$, cắt cạnh $AC$ theo thứ tự tại $M, N$ (h.5)

Tính theo $a$ độ dài của các đoạn thẳng $DM$ và $EN.$

Lời giải chi tiết

Vì $\displaystyle AD = DE = EB$ (gt)

Nên $\displaystyle AD = DE = EB = {1 \over 3}AB$ (1)

Suy ra: $\displaystyle AE = AD + DE = {2 \over 3}AB$           (2)

Xét $∆ ABC$ có $DM // BC$ (gt)

Theo hệ quả định lí Ta-lét ta có:

$\displaystyle {{AD} \over {AB}} = {{DM} \over {BC}}$

$\displaystyle \Rightarrow {{AD} \over {AB}} = {{DM} \over a}$  (3)

Từ (1) và (3) ta có: $\displaystyle {{DM} \over a} = {1 \over 3}$

$\displaystyle \Rightarrow DM = {1 \over 3}a$

Xét $∆ABC$ có $EN // BC$ (gt)

Theo hệ quả định lí Ta-lét ta có:

$\displaystyle {{AE} \over {AB}} = {{EN} \over {BC}}$

$\displaystyle \Rightarrow {{AE} \over {AB}} = {{EN} \over a}$          (4)

Từ (2) và (4) ta có: $\displaystyle {{EN} \over a} = {2 \over 3}$

$\displaystyle\Rightarrow EN = {2 \over 3}a$

HocTot.Nam.Name.Vn