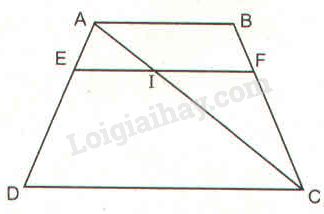
Bài 11 trang 85 SBT toán 8 tập 2Giải bài 11 trang 85 sách bài tập toán 8. Cho hình thang ABCD (AB // CD). Trên cạnh bên AD lấy điểm E sao cho AE/ED = p/q ... Đề bài Cho hình thang \(ABCD \;(AB // CD).\) Trên cạnh bên \(AD\) lấy điểm \(E\) sao cho \(\displaystyle {{AE} \over {ED}} = {p \over q}\). Qua \(E\) kẻ đường thẳng song song với các đáy và cắt \(BC\) tại \(F\). Chứng minh rằng: \(\displaystyle EF = {{p.CD + q.AB} \over {p + q}}\) HD: Kẻ thêm đường chéo \(AC\), cắt \(EF\) ở \(I\), rồi áp dụng hệ quả định lí Ta-lét vào các tam giác \(ADC\) và \(CAB.\)
Phương pháp giải - Xem chi tiết - Định lí Ta-lét: Nếu một đường thẳng song song với một cạnh của tam giác và cắt hai cạnh còn lại thì nó định ra trên hai cạnh ấy những đoạn thẳng tương ứng tỉ lệ. - Hệ quả định lí Ta-lét: Nếu một đường thẳng cắt hai cạnh còn lại của một của một tam giác và song song với các cạnh còn lại thì nó tạo thành một tam giác mới có ba cạnh tương ứng tỉ lệ với ba cạnh còn lại của tam giác đã cho. - Tính chất tỉ lệ thức: \(\dfrac{a}{b} = \dfrac{c}{d} \Rightarrow \dfrac{a}{{a + b}} = \dfrac{c}{{c + d}}\) Lời giải chi tiết
Kẻ đường chéo \(AC\) cắt \(EF\) tại \(I.\) Áp dụng hệ quả định lí Ta-lét vào \(\Delta ADC \) có \(EI // CD\), ta có: \(\displaystyle {{AE} \over {AD}} = {{EI} \over {CD}}\) \( \Rightarrow \displaystyle EI = {{AE} \over {AD}}.CD\) (1) Lại có: \(\displaystyle {{AE} \over {ED}} = {p \over q}\) (gt) Áp dụng tính chất của tỉ lệ thức ta có: \(\displaystyle {{AE} \over {ED}} = {p \over q}\) \( \displaystyle\Rightarrow {{AE} \over {AE + ED}} = {p \over {p + q}}\) Hay \( \displaystyle{{AE} \over {AD}} = {p \over {p + q}}\) (2) Từ (1) và (2) suy ra: \(\displaystyle EI = {p \over {p + q}}.CD\) Áp dụng định lí Ta-lét vào \(\Delta ABC\) có \(IF // AB\), ta có: \(\displaystyle {{BF} \over {FC}} = {{AI} \over {IC}}\) (3) Áp dụng định lí Ta-lét vào \(\Delta ADC\) có \(EI // CD\), ta có: \(\displaystyle {{AE} \over {ED}} = {{AI} \over {IC}}\) (4) Từ (3) và (4) suy ra: \(\displaystyle {{BF} \over {FC}} = {{AE} \over {ED}} = {p \over q}\) Áp dụng hệ quả định lí Ta-lét vào \(\Delta ABC\) có \(IF // AB\), ta có: \(\displaystyle {{IF} \over {AB}} = {{CF} \over {CB}}\) \(\displaystyle \Rightarrow IF = {{CF} \over {CB}}.AB\) (5) Ta có: \(\displaystyle {{BF} \over {CF}} = {p \over q}\) (cmt) \(\displaystyle \Rightarrow {{CF} \over {BF}} = {q \over p}\) Áp dụng tính chất của tỉ lệ thức ta có: \(\displaystyle {{CF} \over {BF}} = {q \over p}\) \(\displaystyle \Rightarrow {{CF} \over {CF + BF}} = {q \over {p + q}} \) \(\displaystyle \Rightarrow {{CF} \over {CB}} = {q \over {p + q}}\) (6) Từ (5) và (6) suy ra: \(\displaystyle IF = {q \over {p + q}}.AB\) Vậy \(\displaystyle EF = EI + {\rm I}F \)\(\,\displaystyle = {p \over {p + q}}.CD + {q \over {p + q}}.AB \)\(\,\displaystyle = {{p.CD + q.AB} \over {p + q}}\) HocTot.Nam.Name.Vn  Chia sẻ Bình luận
Tham Gia Group Dành Cho 2K11 Chia Sẻ, Trao Đổi Tài Liệu Miễn Phí
|
