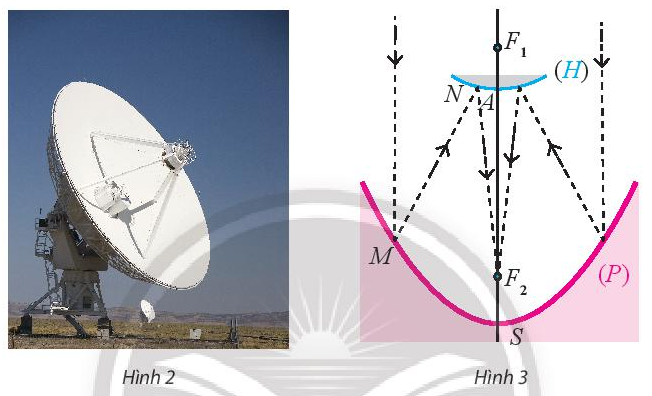
Giải bài 6 trang 65 Chuyên đề học tập Toán 10 – Chân trời sáng tạoTa đã biết tính chất quang học của ba đường conic (xem phần đọc thêm Bạn có biết? ở trang 72, sách giáo khoa Toán 10, tập hai). Tổng hợp đề thi học kì 1 lớp 10 tất cả các môn - Chân trời sáng tạo Toán - Văn - Anh - Lí - Hóa - Sinh - Sử - Địa... Đề bài Ta đã biết tính chất quang học của ba đường conic (xem phần đọc thêm Bạn có biết? ở trang 72, sách giáo khoa Toán 10, tập hai). Hypebol cũng có tính chất quang học tương tự như elip: Tia sáng hướng tới tiêu điểm \({F_1}\) của hypebol (H) khi gặp một nhánh của (H) sẽ cho tia phản xạ đi qua \({F_2}\). Một nhà nghiên cứu thiết kế một kính thiên văn vô tuyến chứa hai gương có mặt cắt hình parabol (P) và hình một nhánh của hypebol (H). Parabol (P) có tiêu điểm \({F_1}\) và đỉnh S. Hypebol (H) có đỉnh A, có chung một tiều điểm là \({F_1}\) với (P) và còn có tiêu điểm thứ hai \({F_2}\) (Hình 3). Nguyên tắc hoạt động của kính thiên văn đó như sau: Tin hiệu đến từ vũ trụ được xem như song song với trục của parabol (P), khi đến điểm M của (P) sẽ cho tia phản xa theo hướng \(M{F_1}\) , tia này gặp (H) tại điểm Nvà cho tia phản xạ tới \({F_2}\) là nơi thu tín hiệu. Cho biết \(S{F_1} = 14{\rm{ }}m,{\rm{ }}S{F_2} = 2m\)và \(A{F_1} = 1m\). Hãy viết phương trình chính tắc của (P) và (H). (Nguồn: https://sciencestruck.com/parabolic-mirror-working-principle-applications)
Phương pháp giải - Xem chi tiết Hypebol (H) \(\frac{{{x^2}}}{{{a^2}}} - \frac{{{y^2}}}{{{b^2}}} = 1\) có tiêu điểm \({F_1}( - c;0),{F_2}(c;0),\) Parabol (P) \({y^2} = 2px\) có tiêu điểm: \(F\left( {\frac{p}{2};0} \right)\) Lời giải chi tiết Gọi phương trình chính tắc của parabol (P) là \({y^2} = 2px\) PTCT của (H) là \(\frac{{{x^2}}}{{{a^2}}} - \frac{{{y^2}}}{{{b^2}}} = 1\) Ta có: tiêu điểm \(\left( {\frac{p}{2};0} \right)\) của (P) là \({F_2}\) \( \Rightarrow S{F_2} = \frac{p}{2} \Rightarrow p = 4 \Rightarrow (P):{y^2} = 8x\) Lại có: Tiêu cự của (H) là \(2c = {F_1}{F_2} = S{F_1} - S{F_2} = 12 \Rightarrow c = 6\) Mà \(a = \frac{A{F_2} - A{F_1}}2= c - A{F_1} = 6 - 1 = 5;{b^2} = \sqrt {{c^2} - {a^2}} = 11\) Vậy phương trình của (H) là \(\frac{{{x^2}}}{{25}} - \frac{{{y^2}}}{{11}} = 1\)
|