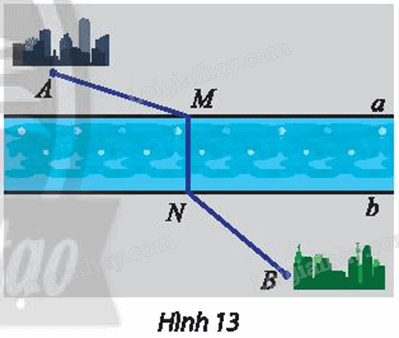
Giải bài 6 trang 19 Chuyên đề học tập Toán 11 Chân trời sáng tạoHai thành phố A, B nằm ở hai bên bờ của một con sông (Hình 13). Tổng hợp đề thi học kì 2 lớp 11 tất cả các môn - Chân trời sáng tạo Toán - Văn - Anh - Lí - Hóa - Sinh Đề bài Hai thành phố A, B nằm ở hai bên bờ của một con sông (Hình 13). Giả sử hai bờ sông là hai đường thẳng song song a, b. Tìm vị trí điểm M bên bờ a và N bên bờ b để xây dựng một chiếc cầu MN sao cho MN vuông góc với a, b và tổng khoảng cách AM + NB ngắn nhất.
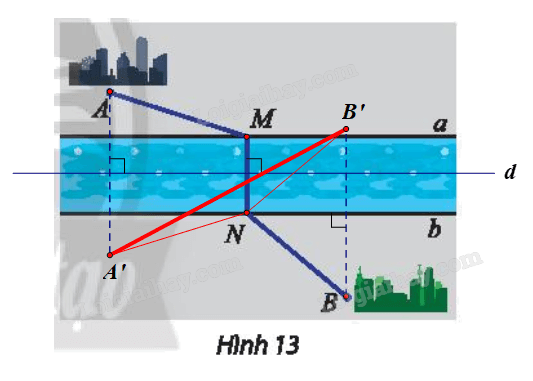
Phương pháp giải - Xem chi tiết Ta đi chứng minh tổng khoảng cách AM+NB ngắn nhất khi và chỉ khi A′N+NB′=A′B′. Với A’, B’ là ảnh của A, B qua Đd (d là đường trung trực của đoạn MN) Quảng cáo  Lời giải chi tiết
Gọi d là đường trung trực của đoạn MN. Suy ra điểm N là ảnh của điểm M qua Đd Lấy điểm A’ là ảnh của điểm A qua Đd Suy ra đoạn A’N là ảnh của đoạn AM qua Đd Do đó A′N=AM. Lấy điểm B’ là ảnh của điểm B qua Suy ra b là đường trung trực của đoạn BB’. Mà N∈b (giả thiết). Do đó NB′=NB. Ta có AM+NB=A′N+NB′. Áp dụng bất đẳng thức tam giác cho ∆A’NB’, ta được: A′N+NB′≥A′B′. Do đó tổng khoảng cách AM+NB ngắn nhất khi và chỉ khi A′N+NB′=A′B′. Tức là, ba điểm A’, N, B’ thẳng hàng. Vậy N là giao điểm của A’B’ và bờ b, M là điểm nằm bên bờ a thỏa mãn M = Đd(N), với d là đường trung trực của đoạn MN, A′=Đd(A),B′=Đb(B).  Chia sẻ Bình luận
Group 2K8 ôn Thi ĐGNL & ĐGTD Miễn Phí
>> 2K8 Chú ý! Lộ Trình Sun 2026 - 3IN1 - 1 lộ trình ôn 3 kì thi (Luyện thi 26+TN THPT, 90+ ĐGNL HN, 900+ ĐGNL HCM; 70+ ĐGTD - Click xem ngay) tại Tuyensinh247.com.Đầy đủ theo 3 đầu sách, Thầy Cô giáo giỏi, 3 bước chi tiết: Nền tảng lớp 12; Luyện thi chuyên sâu; Luyện đề đủ dạng đáp ứng mọi kì thi.
|
