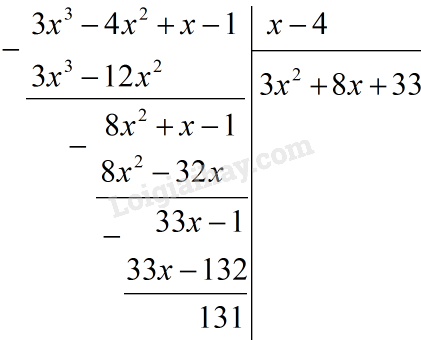Bài 57 trang 38 SBT toán 8 tập 1Giải bài 57 trang 38 sách bài tập toán 8. Tìm giá trị nguyên của biến x để tại đó giá trị của mỗi biểu thức sau là một số nguyên ...
Lựa chọn câu để xem lời giải nhanh hơn
Tìm giá trị nguyên của biến \(x\) để tại đó giá trị của mỗi biểu thức sau là một số nguyên : LG a \(\displaystyle {2 \over {x - 3}}\) Phương pháp giải: - Tìm điều kiện xác định của các phân thức. - Biến đổi biểu thức về dạng đơn giản. - Để phân thức có giá trị là một số nguyên thì tử thức phải chia hết cho mẫu thức. - Vận dụng kiến thức về ước đã học, tìm giá trị của \(x\). Lời giải chi tiết: \(\displaystyle {2 \over {x - 3}}\) là một số nguyên nên \(2 \vdots \left( {x - 3} \right)\) và \(x \ne 3\) \(\Rightarrow x – 3 ∈ Ư(2) = \{ - 2; -1 ; 1; 2 \}\) \(\eqalign{& x - 3 = - 2 \Rightarrow x = 1 (tm) \cr & x - 3 = - 1 \Rightarrow x = 2(tm) \cr & x - 3 = 1 \Rightarrow x = 4 (tm) \cr & x - 3 = 2 \Rightarrow x = 5(tm) \cr} \) Vậy với \(x ∈ \{ 1; 2; 4; 5 \}\) thì \(\displaystyle {2 \over {x - 3}}\) là một số nguyên. LG b \(\displaystyle {3 \over {x + 2}}\) Phương pháp giải: - Tìm điều kiện xác định của các phân thức. - Biến đổi biểu thức về dạng đơn giản. - Để phân thức có giá trị là một số nguyên thì tử thức phải chia hết cho mẫu thức. - Vận dụng kiến thức về ước đã học, tìm giá trị của \(x\). Lời giải chi tiết: \(\displaystyle {3 \over {x + 2}}\) là một số nguyên nên \(3 \vdots (x + 2)\) và \(x ≠ - 2\) \(\Rightarrow x + 2 ∈ Ư(3) = \{ -3; -1; 1; 3 \}\) \(\eqalign{ & x + 2 = - 3 \Rightarrow x = - 5 (tm) \cr & x + 2 = - 1 \Rightarrow x = - 3 (tm) \cr & x + 2 = 1 \Rightarrow x = - 1(tm) \cr & x + 2 = 3 \Rightarrow x = 1(tm) \cr} \) Vậy với \(x ∈ \{ -5; -3; -1; 1 \}\) thì \(\displaystyle {3 \over {x + 2}}\) là một số nguyên LG c \(\displaystyle {{3{x^3} - 4{x^2} + x - 1} \over {x - 4}}\) Phương pháp giải: - Tìm điều kiện xác định của các phân thức. - Biến đổi biểu thức về dạng đơn giản. - Để phân thức có giá trị là một số nguyên thì tử thức phải chia hết cho mẫu thức. - Vận dụng kiến thức về ước đã học, tìm giá trị của \(x\). Lời giải chi tiết: Đặt phép tính chia:
Từ phép chia trên ta có: \(\displaystyle {{3{x^3} - 4{x^2} + x - 1} \over {x - 4}}\)\(\displaystyle = {{\left( {3{x^2} + 8x + 33} \right)\left( {x - 4} \right) + 131} \over {x - 4}}\)\(\displaystyle = 3{x^2} + 8x + 33 + {{131} \over {x - 4}}\) Với \(x\) là số nguyên ta có : \(3{x^2} + 8x + 33\) là số nguyên Vậy muốn biểu thức là số nguyên thì \(131 \vdots (x – 4 )\) và \(x ≠ 4\) \(\Rightarrow x – 4 ∈ Ư(131) = \{-131; -1; 1;\)\( 131\}\) \(\eqalign{ & x - 4 = - 131 \Rightarrow x = - 127(tm) \cr & x - 4 = - 1 \Rightarrow x = 3 (tm) \cr & x - 4 = 1 \Rightarrow x = 5 (tm)\cr & x - 4 = 131 \Rightarrow x = 135(tm) \cr} \) Vậy \(x ∈ \{-127; 3; 5; 135\}\) thì \(\displaystyle {{3{x^3} - 4{x^2} + x - 1} \over {x - 4}}\) là số nguyên LG d \(\displaystyle {{3{x^2} - x + 1} \over {3x + 2}}\) Phương pháp giải: - Tìm điều kiện xác định của các phân thức. - Biến đổi biểu thức về dạng đơn giản. - Để phân thức có giá trị là một số nguyên thì tử thức phải chia hết cho mẫu thức. - Vận dụng kiến thức về ước đã học, tìm giá trị của \(x\). Lời giải chi tiết: Ta có: \(\displaystyle {{3{x^2} - x + 1} \over {3x + 2}}\) \(\begin{array}{l} \(\displaystyle = {{\left( {3x + 2} \right)\left( {x - 1} \right) + 3} \over {3x + 2}}\)\(\displaystyle = x - 1 + {3 \over {3x + 2}}\) (với \(x \ne \displaystyle - {3 \over 2}\) ) \(x\) là số nguyên nên \(x – 1\) là số nguyên. Vậy muốn biểu thức đã cho là số nguyên thì \(3 ⋮ (3x + 2)\) và \(x \ne \displaystyle - {3 \over 2}\) \(3x + 2 ∈ Ư(3) = \{-3; -1; 1; 3 \}\) \(3x + 2 = - 3 \Rightarrow x = \displaystyle - {5 \over 3}\) (loại) \(3x + 2 = - 1 \Rightarrow x = - 1(tm)\) \(3x + 2 = 1 \Rightarrow x = \displaystyle - {1 \over 3} \) (loại) \(3x + 2 = 3 \Rightarrow x = \displaystyle {1 \over 3} \) (loại) Vậy với \(x = - 1\) thì biểu thức \(\displaystyle {{3{x^2} - x + 1} \over {3x + 2}}\) có giá trị nguyên. HocTot.Nam.Name.Vn
|