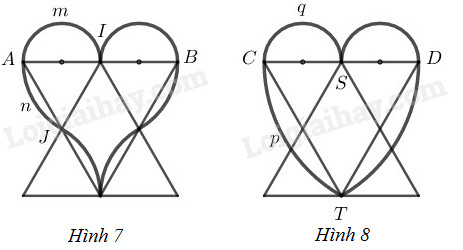
Bài 57 trang 110 SBT toán 9 tập 2

Đề bài

Các tam giác trong hai hình quả tim dưới đây \((h.7\) và \(h.8)\) đều là tam giác đều. Biết \(AB = CD = 8cm.\) Tính chu vi của mỗi hình quả tim. 

Lời giải chi tiết

Hình \(7\) có \(2\) nửa đường tròn đường kính \(4 cm\) và có 4 cung có độ dài là \(\displaystyle {1 \over 6}\) đường tròn bán kính \(4 cm\) 

\(\overparen{AmI}\) là nửa đường tròn đường kính \(4 cm\), gọi độ dài cung này là \({l_1}\), có 2 cung như thế. 

\({l_1} = \displaystyle {1 \over 2}\pi .4 = 2\pi \) (cm)

\(\overparen{AnJ}\) là cung \(\displaystyle {1 \over 6}\) đường tròn bán kính \(4 cm\) (trên hình 7 có \(4\) cung bằng nhau (vì \(4\) đường tròn đó có cùng bán kính)) 

Gọi \(\overparen{AnJ}\) có độ dài \({l_2}\)

\({l_2} = \displaystyle {1 \over 6}.2\pi .4 = {4 \over 3}\pi \) \((cm)\)

Chu vi hình \(7\) là: \(2.{l_1} + 4.{l_2}\)\(=2\pi .2 + \displaystyle {4 \over 3}\pi .4 = \displaystyle {{28} \over 3}\pi \) \((cm)\)

Hình \(8\) có hai nửa đường tròn đường kính \(4 cm\) và hai cung \(\displaystyle {1 \over 6}\) đường tròn bán kính \(8 cm\)

Cung \(\overparen{CpS}\) là nửa đường tròn đường kính \(4 cm\) có độ dài \({l_1}\)

\({l_1} = \displaystyle {1 \over 2}.\pi .4 = 2\pi \) (cm)

Cung \(\overparen{CqT}\) là \(\displaystyle {1 \over 6}\) đường tròn bán kính \(8 cm\) có độ dài \({l_2}\)

\({l_2} = \displaystyle {1 \over 6}.2\pi .8 = {8 \over 3}\pi \) \((cm)\)

Chu vi hình \(8\) bằng: \(2.{l_1} + 2.{l_2} = 2.2\pi  + 2.\displaystyle {8 \over 3}\pi  =\displaystyle  {{28} \over 3}\pi \) \((cm)\)

HocTot.Nam.Name.Vn