Bài 60 trang 110 SBT toán 9 tập 2Giải bài 60 trang 110 sách bài tập toán 9. Cho tam giác cân ABC có ... Tổng hợp Đề thi vào 10 có đáp án và lời giải Toán - Văn - Anh Đề bài Cho tam giác cân \(ABC\) có \(\widehat B = {120^\circ},\) \(AC = 6cm.\) Tính độ dài đường tròn ngoại tiếp tam giác đó. Phương pháp giải - Xem chi tiết Ta sử dụng kiến thức: +) Trong tam giác cân, hai góc ở đáy bằng nhau. +) Trong giác cân, đường cao ứng với cạnh đáy cũng là đường trung tuyến ứng với cạnh đáy. +) Trong một đường tròn, góc nội tiếp (nhỏ hơn hoặc bằng \(90^\circ\)) có số đo bằng nửa số đo của góc ở tâm cùng chắn một cung. +) Độ dài \(C\) của một đường tròn bán kính \(R\) được tính theo công thức: \(C=2\pi R\) Lời giải chi tiết
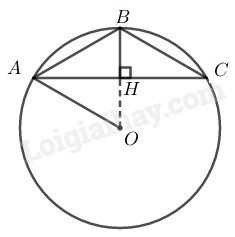
Vẽ đường tròn \((O)\) ngoại tiếp tam giác \(ABC\) \(∆ABC\) cân có \(\widehat B = 120^\circ \) nên \(∆ABC\) cân tại \(B\) \( \Rightarrow \widehat A = \widehat C = \displaystyle {{{{180}^\circ} - \displaystyle {{120}^\circ}} \over 2} = {30^0}\) Kẻ \(BH \bot AC\)\( \Rightarrow AH = HC = \displaystyle {1 \over 2}AC = 3\) \((cm)\) Trong tam giác vuông \(BHA\) ta có \(\widehat {BHA} = {90^0}\) có: \(AB =\displaystyle {{AH} \over {\cos A}} \)\(=\displaystyle {3 \over {\cos {{30}^0}}} \)\(= \displaystyle {3 \over {\displaystyle {{\sqrt 3 } \over 2}}}\)\(= 2\sqrt 3 \;\;(cm)\) Xét đường tròn \((O)\) có: \(\widehat C = \displaystyle {1 \over 2}\widehat {AOB}\) (hệ quả góc nội tiếp) \( \Rightarrow \widehat {AOB} = 2\widehat C = {2.30^0} = {60^0}\) \(OA = OB\) (bán kính) Suy ra \(∆AOB\) đều nên \(OA = OB = 2\sqrt 3 \; (cm)\) Độ dài đường tròn ngoại tiếp \(∆ABC\) \(C = 2\pi R\)\( = 2\pi .2\sqrt 3 = 4\pi \sqrt 3 \) \((cm)\) HocTot.Nam.Name.Vn  Chia sẻ Bình luận
Tham Gia Group 2K10 Ôn Thi Vào Lớp 10 Miễn Phí
|
