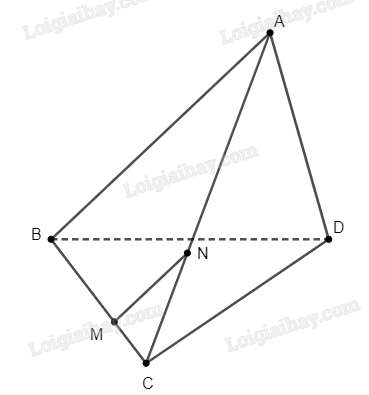
Giải bài 54 trang 118 sách bài tập toán 11 - Cánh diều

Đề bài

Cho tứ diện \(ABCD\). Trên cạnh \(BC\) lấy điểm \(M\) sao cho \(MB = 2MC\). Mặt phẳng \(\left( P \right)\) đi qua \(M\) và song song với mặt phẳng \(\left( {ABD} \right)\) cắt cạnh \(AC\) tại \(N\). Tỉ số \(\frac{{AN}}{{NC}}\) bằng:

A. \(\frac{1}{2}\)                             

B. \(1\)                          

C. \(2\)                          

D. \(3\)

Lời giải chi tiết

Nhận xét rằng \(MN\) chính là giao tuyến của mặt phẳng \(\left( P \right)\) và \(\left( {ABC} \right)\).

Ta nhận thấy rằng \(AB\) là giao tuyến của \(\left( {ABD} \right)\) và \(\left( {ABC} \right)\).

Do \(\left( P \right)\) song song với \(\left( {ABD} \right)\), ta suy ra \(MN\parallel AB\).

Tam giác \(ABC\) có \(MN\parallel AB\), nên theo định lí Thales, ta có \(\frac{{AN}}{{NC}} = \frac{{BM}}{{MC}} = 2\).

Vậy đáp án đúng là C.