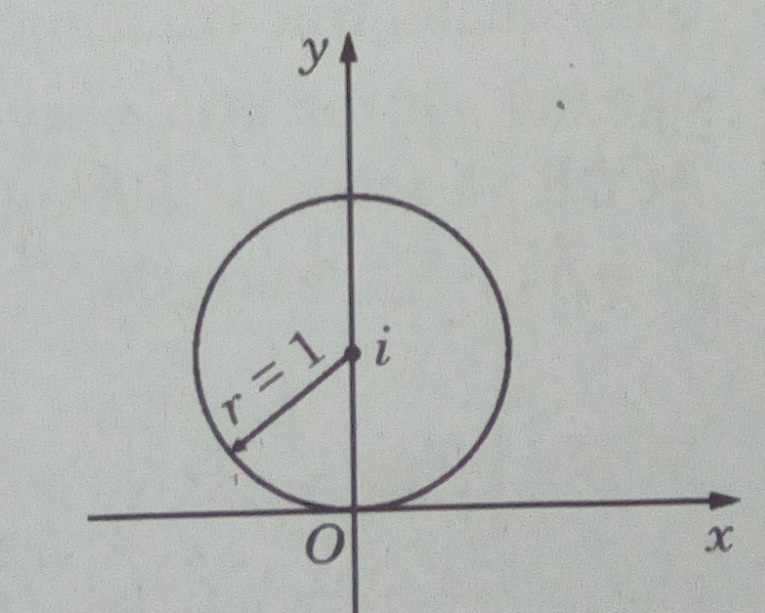Bài 22 trang 219 SBT giải tích 12

LG a

|z – i| = 1

Lời giải chi tiết:

Gọi \(z = x + yi\left( {x,y \in \mathbb{R}} \right)\) ta được:

\(\begin{array}{l}
\left| {x + yi - i} \right| = 1\\
\Leftrightarrow \left| {x + \left( {y - 1} \right)i} \right| = 1\\
\Leftrightarrow \sqrt {{x^2} + {{\left( {y - 1} \right)}^2}} = 1\\
\Leftrightarrow {x^2} + {\left( {y - 1} \right)^2} = 1
\end{array}\)

Vậy tập hợp các điểm là đường tròn bán kính bằng 1 và tâm là điểm (0; 1)

LG b

|2 + z| < |2 – z|

Lời giải chi tiết:

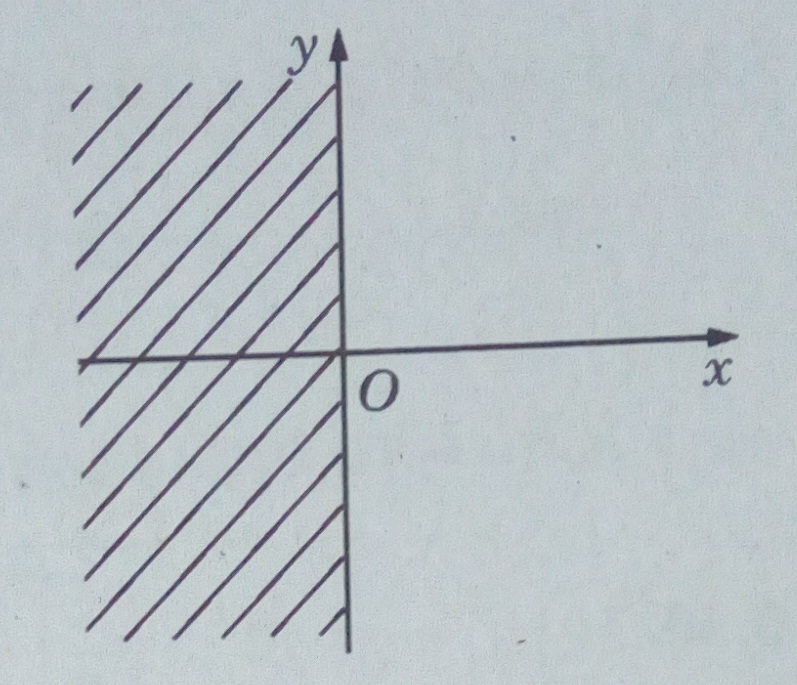
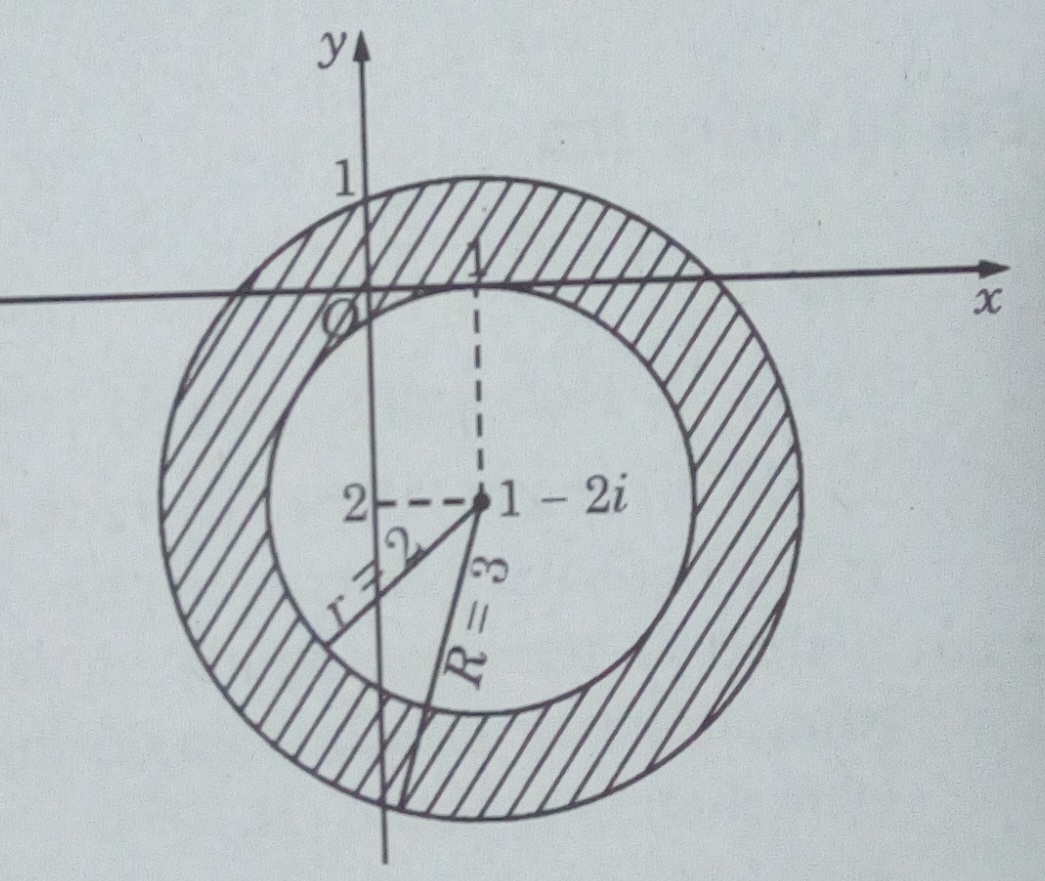
Ta có: \(|2 + z{|^2} < |2 - z{|^2}\)

\(\Leftrightarrow |(2 + x) + iy{|^2} < |(2 - x) - iy{|^2}\)

\(\Leftrightarrow {(2 + x)^2} + {y^2} < {(2 - x)^2} + {( - y)^2}\)

\(\Leftrightarrow x < 0\)

Đó là tập hợp các số phức có phần thực nhỏ hơn 0, tức là nửa trái của mặt phẳng tọa độ không kể trục Oy.

LG c

\(2 \le |z - 1 + 2i| < 3\)

Lời giải chi tiết:

Gọi \(z = x + yi\left( {x,y \in \mathbb{R}} \right)\) ta được:

\(\begin{array}{l}2 \le \left| {x + yi - 1 + 2i} \right| < 3\\ \Leftrightarrow 2 \le \left| {\left( {x - 1} \right) + \left( {y + 2} \right)i} \right| < 3\\ \Leftrightarrow 2 \le \sqrt {{{\left( {x - 1} \right)}^2} + {{\left( {y + 2} \right)}^2}}  < 3\\ \Leftrightarrow 4 \le {\left( {x - 1} \right)^2} + {\left( {y + 2} \right)^2} < 9\end{array}\)

Vậy tập hợp điểm cần tìm là hình vành khăn kể cả biên trong. Đó là những điểm (x; y) trên mặt phẳng tọa độ thỏa mãn điều kiện:  \(4 \le {(x - 1)^2} + {(y + 2)^2} < 9\)

HocTot.Nam.Name.Vn