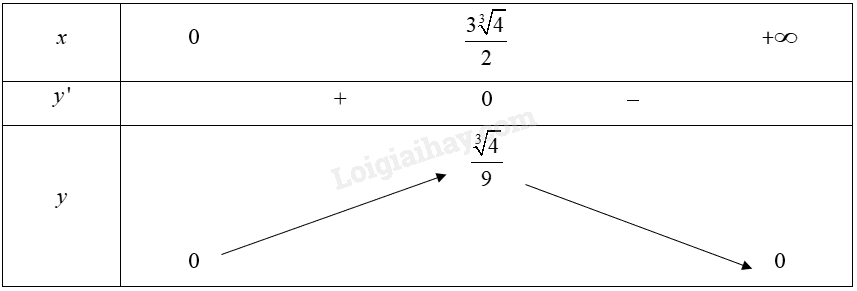
Giải bài 46 trang 20 sách bài tập toán 12 - Cánh diềuNồng độ \(C\) của một loại hoá chất trong máu sau \(t\) giờ tiêm vào cơ thể được cho bởi công thức: \(C\left( t \right) = \frac{{3t}}{{27 + {t^3}}}\) với \(t \ge 0\) (Nguồn: R. Larson and B. Edwards, Calculus 10e, Cengage 2014). Sau khoảng bao nhiêu giờ tiêm thì nồng độ của hoá chất trong máu là cao nhất? Tổng hợp đề thi học kì 1 lớp 12 tất cả các môn - Cánh diều Toán - Văn - Anh - Lí - Hóa - Sinh - Sử - Địa Đề bài Nồng độ \(C\) của một loại hoá chất trong máu sau \(t\) giờ tiêm vào cơ thể được cho bởi công thức: \(C\left( t \right) = \frac{{3t}}{{27 + {t^3}}}\) với \(t \ge 0\) (Nguồn: R. Larson and B. Edwards, Calculus 10e, Cengage 2014). Sau khoảng bao nhiêu giờ tiêm thì nồng độ của hoá chất trong máu là cao nhất? Phương pháp giải - Xem chi tiết Xét hàm số \(C\left( t \right)\) trên nửa khoảng \(\left[ {0; + \infty } \right)\), lập bảng biến thiên và tìm giá trị lớn nhất của hàm số. Lời giải chi tiết Xét hàm số \(C\left( t \right) = \frac{{3t}}{{27 + {t^3}}}\) trên nửa khoảng \(\left[ {0; + \infty } \right)\). Ta có: \(C'\left( t \right) = \frac{{{{\left( {3t} \right)}^\prime }.\left( {27 + {t^3}} \right) - \left( {3t} \right).{{\left( {27 + {t^3}} \right)}^\prime }}}{{{{\left( {27 + {t^3}} \right)}^2}}} = \frac{{3\left( {27 + {t^3}} \right) - \left( {3t} \right).3{t^2}}}{{{{\left( {27 + {t^3}} \right)}^2}}} = \frac{{81 - 6{{\rm{x}}^3}}}{{{{\left( {27 + {t^3}} \right)}^2}}}\) \(C'\left( t \right) = 0\) khi \(t = \frac{{3\sqrt[3]{4}}}{2}\). Bảng biến thiên của hàm số:
Căn cứ vào bảng biến thiên, ta có: \(\mathop {\max }\limits_{\left( {0;4} \right)} C\left( t \right) = \frac{{\sqrt[3]{4}}}{9}\) tại \(t = \frac{{3\sqrt[3]{4}}}{2}\). Vậy sau khoảng \(t = \frac{{3\sqrt[3]{4}}}{2} \approx 2,38\) giờ thì nồng độ của hoá chất trong máu là cao nhất.
|