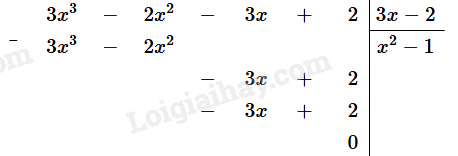Giải bài 45 trang 54 sách bài tập toán 7 - Cánh diềuCho đa thức (P(x) = 3{x^3} - 2{x^2} + 5). Chia đa thức P(x) cho đa thức Q(x) (Q(x) ≠ 0) được thương là đa thức S(x)= 3x – 2 và dư là đa thức R(x) = 3x + 3. Tìm đa thức Q(x). Tổng hợp đề thi học kì 2 lớp 7 tất cả các môn - Cánh diều Toán - Văn - Anh - Khoa học tự nhiên... Đề bài Cho đa thức \(P(x) = 3{x^3} - 2{x^2} + 5\). Chia đa thức P(x) cho đa thức Q(x) (Q(x) ≠ 0) được thương là đa thức S(x)= 3x – 2 và dư là đa thức R(x) = 3x + 3. Tìm đa thức Q(x). Phương pháp giải - Xem chi tiết Bước 1: Biểu diễn đa thức Q(x) theo P(x), S(x) và R(x) Bước 2: Thực hiện các phép toán cộng/trừ/nhân/chia đa thức theo quy tắc để tính Q(x) Lời giải chi tiết Theo đề bài ta có: P(x) : Q(x) = S(x) và dư R(x). Khi đó \(P(x) - R(x) = S(x).Q(x)\) Xét \(P(x) - R(x) = (3{x^3} - 2{x^2} + 5) - (3x + 3) = 3{x^3} - 2{x^2} + 5 - 3x - 3 = 3{x^3} - 2{x^2} - 3x + 2\) Suy ra \(Q(x) = (3{x^3} - 2{x^2} - 3x + 2):S(x) = (3{x^3} - 2{x^2} - 3x + 2):(3x - 2)\)
Vậy \(Q(x) = {x^2} - 1\)
|